Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 59
Simplifique a equação dada por uma rotação e uma translação de eixos. Faça um esboço do gráfico e mostre os três conjuntos de eixos.
Passo 1
Chegamos em um ponto das cônicas que elas além de não estarem fora do centro, elas estão “tortas”, ou seja, rotacionaram em torno do centro. A primeira coisa que devemos saber aqui é qual o formato dessa cônica. Vamos para uma regrinha bem básica. As cônicas em rotação vão obedecer a esse formato de equação (B diferente de 0).
Em que:
Sendo a o ângulo de rotação.
Após rotação, a nossa função assume parâmetros x‘ e y’. E temos mais um conjunto de relações.
Sabendo disso, bora ANIQUILAR essa questão!
Passo 2
Antecipando pra vocês, essas questões exigem uma álgebra um pouco mais apurada que o normal, por isso, vamos com calma.
Para essa questão, temos que:
Logo,
Passo 3
Vamos para a nossa outra transformação.
E agora substituímos na nossa equação principal para acharmos a nossa equação com rotação.
Gerando esse esboço:
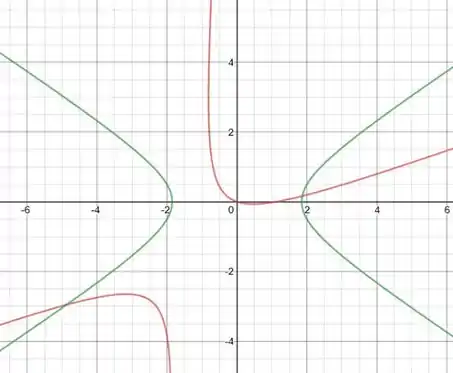
Em verde a hipérbole antes da rotação e em vermelho após a rotação e translação.