Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 70
Ache uma equação da reta que passa por (2,5) e faz com a reta 3x - 4y + 7 = 0 um ângulo cuja medida em radianos é .
Passo 1
Neste problema, sabendo a equação da Reta 1 (3x - 4y + 7 = 0) queremos obter a equação da Reta 2 que forma com a primeira um ângulo de e que passa pelo ponto P (2,5).
Para começar, vamos desenhar a situação.
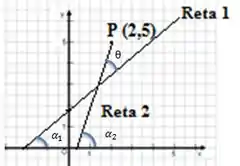
Sendo assim podemos tirar duas conclusões:
E reorganizando a equação da Reta 1:
Com estes dados podemos obter a inclinação da reta 2 e sua equação.
Passo 2
Antes de obter a equação da reta precisamos achar a inclinação da reta 2. O Teorema 1.6.7 nos diz que:
Com esse teorema podemos obter o ângulo a partir da inclinação para a reta 1:
O ângulo é calculado obtendo o arco tangente de 0,75:
Em radianos:
Podemos dizer que o ângulo entre as retas é a diferença do ângulo e :
Sendo assim:
Então:
Passo 3
Com a inclinação podemos obter a equação da reta 2, que passa pelo ponto P.
Sabendo que essa equação pode ser dada por:
Substituindo os pontos de P e a inclinação:
Rearranjando:
Resposta
A equação da reta é: