Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.1 - Ex. 3
Em cada parte da figura abaixo, determine se o gráfico define como função de
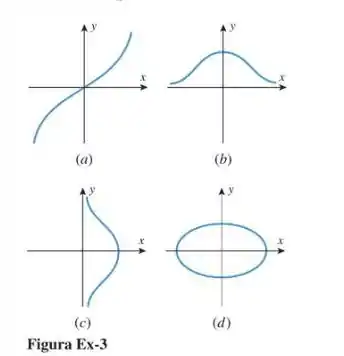
Passo 1
Show, vamos relembrar a nossa definiçãozinha
Se uma variável depende de uma variável de tal modo que cada valor de determina exatamente um valor de , então dizemos que é uma função de
Ou seja, para cada valor de só podemos ter um valor de
Vamos ver isso daí, para fazer isso, vamos imaginar varias retas verticais, se elas so baterem em um ponto da função show! O grafico define como função de , se não não define
Passo 2
Na letra e na ta tudo certo, para cada valor de só temos um valor de
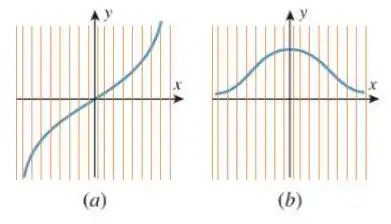
Entao nessas letras o gráfico define como função de
Passo 3
Agora nas letras e não podemos dizer a mesma coisa hehe se liga
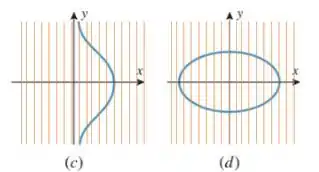
Aqui, temos algumas linhas que batem mais de uma vez no gráfico! Entao nessas letras o gráfico não define como função de
Resposta
Ei, a resposta está no passo a passo :)