Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.1 - Ex. 25
Conforme mostra a figura abaixo, um pendulo de comprimento constante L faz um ângulo com a sua posição vertical. Expresse a altura como uma função do ângulo .
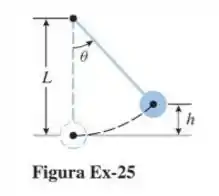
Passo 1
Se a gente traçar uma linha na figura desse jeito aqui:
Formamos um triangulo retângulo, como é constante, ele fica assim:
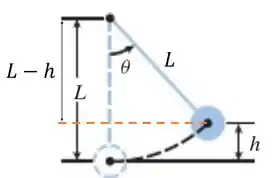
Deixando sozinho, temos que
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Dada G x = x - 2 - x + 2 , expresse G x sem as barras de valor absoluto, se x estiver no intervalo dado: ( - ∞ ,0 )
Dada G x = x - 2 - x + 2 , expresse G x sem as barras de valor absoluto, se x estiver no intervalo dado: [ 2 ,+ ∞ )
Dada f t = 3 + t - t - 3 t , expresse f t sem as barras de valor absoluto, se t estiver no intervalo dado: [ - 3 ,0 )
Dada f t = 3 + t - t - 3 t , expresse f t sem as barras de valor absoluto, se t estiver no intervalo dado: [ 0 ,+ ∞ )
Dada f t = 3 + t - t - 3 t , expresse f t sem as barras de valor absoluto, se t estiver no intervalo dado: - ∞ ,- 3