Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 68e
Ache todos os valores de t no intervalo de para os quais a equação dada é satisfeita:
e)
Passo 1
Queremos obter os ângulos (valores de t) no intervalo de que tenham sua secante igual a .
Para começar é importante lembrar que:
Então:
Racionalizando:
Sendo assim, queremos o ângulo t cujo cosseno seja igual a . E para determiná-lo vamos desenhar nosso circulo trigonométrico, cujo raio é igual a 1.
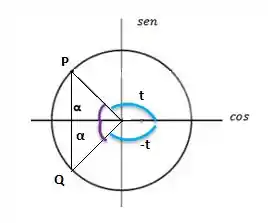
Os valores de cosseno são idênticos para os pontos P e Q, cujos ângulos são e , respectivamente. Então o valor de cosseno igual a poderá ser alcançada quando:
ou
Passo 2
Sabendo os valores que podem ser assumidos pelo t nos resta descobrir qual é o valor do ângulo . Para facilitar a descoberta do ângulo α podemos “espelhar” o ponto P do segundo quadrante no primeiro (P’), como demonstrado na figura abaixo:
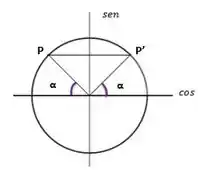
Neste caso teremos o mesmo seno e cossenos opostos. Ou seja:
Pela tabela trigonométrica:
Sendo assim:
Em radianos:
Agora podemos calcular nosso t. Substituindo o valor de
Resposta
ou