Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.7 - Ex. 56

São dadas uma função e um intervalo fechado . Determine se o teorema do valor intermediário se aplica para o valor de dado. Se o teorema for aplicável, ache um número tal que . Caso contrário, explique porquê. Faça um esboço da curva e da reta .

Passo 1

Essa é uma questão para treinarmos a aplicação do teorema do valor intermediário (TVI). Para que o teorema seja aplicável a função deve ser contínua no intervalo fechado . Se essa hipótese for satisfeita, então para todo entre e existirá um tal que .

Devemos então verificar se é contínua e se está entre e . Caso essas duas condições sejam satisfeitas, devemos procurar tal que .

Note que não é definida pata , que está no interior do intervalo . Assim, não é contínua no intervalo e o TVI não é válido!

Passo 2

Se tentarmos achar tal que , não vamos obter sucesso:

Passo 3

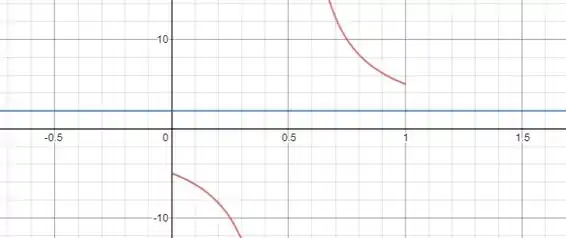
O gráfico de nesse intervalo e da reta :

Resposta

O TVI não é aplicável.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o Teorema do Valor Intermediário para mostrar que existe uma raiz da equação dada no intervalo especificado f x = c o s x = x , ( 0,1 )

Suponha que uma função f seja contínua em 0,1 , exceto em 0,25 , e que f 0 = 1 e f 1 = 3 . Seja N = 2 . Esboce dois gráficos possíveis de f , um indicando que f pode não satisfazer a conclusão do Teor

Use o Teorema do Valor Intermediário para mostrar que existe uma raiz da equação dada no intervalo especificado f ( x ) x 4 + x - 3 = 0 , ( 1,2 )

( a ) Demonstre que a equação tem pelo menos uma raiz real. ( b ) Use sua calculadora para encontrar um intervalo de comprimento 0,01 que contenha a raiz. f x = e x = 2 - x

( a ) Demonstre que a equação tem pelo menos uma raiz real. ( b ) Use sua calculadora para encontrar um intervalo de comprimento 0,01 que contenha a raiz. f x = x 5 - x 2 + 2 x + 3 = 0