Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.1 - Ex. 26

Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo.

G x = - 3   s e n   x ;         0 , 3 π 4

Passo 1

A questão pede para achar os valores máximos e mínimos absolutos da função no intervalo considerado.

A função G x = - 3   s e n   x atinge seu máximo quando s e n   x = - 1 , o que acontece quando

x = 3 π 2 + n ⋅ 2 π ,         n ∈ Z

Já o mínimo é atingido quando s e n   x = 1 , de modo que

x = π 2 + n ⋅ 2 π ,         n ∈ Z

No intervalo [ 0 ,   3 π / 4 ) , apenas o mínimo pode ser atingido quando n = 0 : x = π / 2 . Note que tanto para n = 1 como para n = - 1 , o valor de x não está no intervalo. Como o máximo nunca é atingido nesse intervalo, devemos procura-lo nas extremidades do intervalo.

Passo 2

A seguir damos um esboço do gráfico de G nesse intervalo:

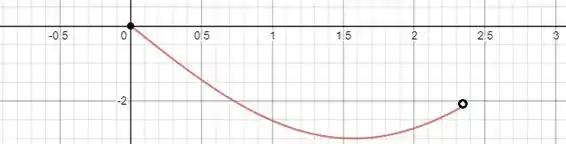
Vemos que de fato o mínimo ocorre para x = π / 2 . O máximo, por sua vez, ocorre na extremidade do intervalo com x = 0 .

Resposta

Máximo absoluto: G 0 = 0 .

Mínimo absoluto: G π / 2 = - 3 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada
Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada
Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada
Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada
Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada