Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo.
Passo 1
A questão pede para achar os valores máximos e mínimos absolutos da função no intervalo considerado.
Note que é uma função definida por partes: para a expressão não está definida, de modo que nesse ponto é definida separadamente de tal forma que . Vemos assim que não é contínua no intervalo, então não podemos garantir que ela terá extremos absolutos mesmo com o intervalo sendo fechado.
Passo 2
A seguir damos um esboço do gráfico de nesse intervalo:
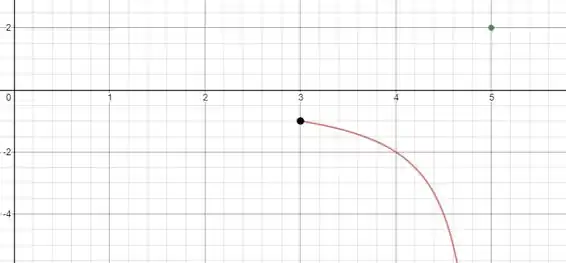
Quando , a função explode para de modo que ela não apresentará mínimo global nesse intervalo.
Eu sei que você deve pensar que o máximo ocorre em com ( o ponto preto no gráfico), mas cuidado: não esqueça o ponto verdinho ali no canto superior direito quando ! O máximo da função ocorre em com , como definido na função.
Resposta
Máximo absoluto: .
Mínimo absoluto: não tem.