Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.1 - Ex. 34

Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo.

F x = U x - U x - 1 ,     o n d e   U x = 0 ,     s e   x < 0 1 ,                 s e   x ≥ 0   ,         ( - 1 ,   1 )

Passo 1

A questão pede para achar os valores máximos e mínimos absolutos da função no intervalo considerado.

Eu sei que você deve estar olhando para essa função com uma cara estranha, ela realmente é! Mas vamos tentar entender como é o seu gráfico. O primeiro passo é escrever U ( x - 1 ) :

U x - 1 = 0 ,       s e   x - 1 < 0 1 ,         s e   x - 1 ≥ 0       ⇒ U x - 1 = 0 ,         s e   x < 1 1 ,           s e   x ≥ 1

Agora precisamos somar U ( x ) com U ( x - 1 ) . Para fazer isso, temos que olhar três intervalos distintos: x < 0 , 0 ≤ x < 1 e x ≥ 1 .

Para x < 0 , temos que U x = 0 e U x - 1 = 0 , de modo que

F x = U x - U x - 1 = 0 - 0 = 0

Já para 0 ≤ x < 1 , temos que U x = 1 e U x - 1 = 0 . Assim,

F x = 1 - 0 = 1

Por fim, para x ≥ 1 , U x = U x - 1 = 1 , de modo que

F x = 1 - 1 = 0

Sendo assim, a função F , na reta real toda, é dada por

F x = 0 ,                         s e   x < 0 1 ,         s e   0 ≤ x < 1 0 ,                           s e   x ≥ 1

Passo 2

No intervalo aberto ( - 1 ,   1 ) , o gráfico de F fica

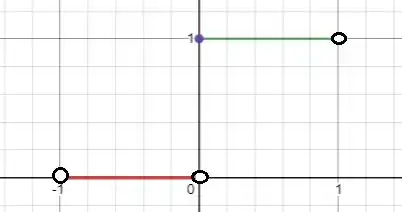
Note que o valor máximo de F é 1 e ocorre no intervalo [ 0 ,   1 ) todo, enquanto o mínimo absoluto é 0 e ocorre no intervalo aberto ( - 1,0 ) todo.

Resposta

Máximo absoluto: F 0 ≤ x < 1 = 1 .

Mínimo absoluto: F - 1 < x < 0 = 0 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada
Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada
Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada
Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada
Nos Exercícios de 1 a 26, ache os extremos relativos da função dada usando o teste da derivada segunda, quando aplicável. Quando ele não for aplicável, use o teste da derivada primeira. Use a derivada