Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.6 - Ex. 19
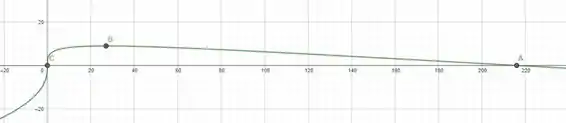
Ache os extermos relativos da função dada usando o teste da derivada segunda, uando aplicável. Quando ele não for aplicável, use o teste da derivada primeira.
Use a derivada segunda para encontrar os pontos de inflexão do gráfico da função e determine onde o gráfico é côncavo para cima e onde é para baixo. Faça um esboço do gráfico.
Passo 1
Vamos começar achandos os pontos críticos da função. Porque eles são os candidatos a extremo. Para isso vamos pegar a derivada de
Os pontos crítos são aqueles que a derivada é ou não existe. Como chegamos em um expoente negativo, a derivada não vai existir quando o .
Isso porque:
Ai, quando o denominador é
Passo 2
Vamos para os outros pontos críticos, que é quando a derivada é .
Fazendo:
E
Vamos ter:
Multiplicando cruzado
Simplificando por
Elevando ao cubo
Esses são os nosso pontos críticos.
Quando não existe a derivada:
Quando a derivada é :
Passo 3
Agora, vamos tentar aplicar o teste da segunda derivada, que vai ser exatamente o que está aqui embaixo, mas só vale para os pontos críticos
Se ou não existir, não funciona o teste.
Vamos ter
Vamos simplificar a expressão colocando em evidência
Temos que ver o valor de para e
Aqui, apareceu novamente o expoente negativo, então a segunda derivada não existe em .
Vamos testar só o .
Aquele no expoente é o mesmo que , então temos:
Logo é ponto de máximo relativo
Passo 4
Vamos aplicar o teste da primeira derivada em
Basicamente, precisamos saber como é a variação de sinal em torno do , organizando isso, colocando em evidência
Já vimos no passo anterior que:
Então, quando for negativo, vamos ter:
Isso porque vai ser negativo e multiplicando por vai dar positivo. Somando com , continua positivo.
Quando for positivo vamos ter
Isso porque só estamos interessados perto do , então aquele termo negativo, continua negativo mas bem pequeno, quando subtrair de não tira muito, fazendo ser perto de
Como não temos troca de sinal, vamos ter que esse ponto não é extremo.
Passo 5
Vamos agora para a concavidade
Vamos analisar direto os sinais dessa função para achar a concavidade e de quebra os pontos de inflexão.
Temos o seguinte quadro de sinais de :
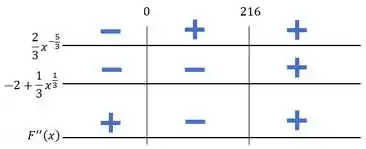
Então, a função é côncava para cima para valores menores que e maiores que , e côncava para baixo entre e .
Assim os pontos de inflexão são:
E
Passo 6
Vamos organizar as informações para o nosso gráfico:
Máximo relativo:
Pontos de inflexão:
Concava para cima:
Concava para baixo
O esboço vai ficar:
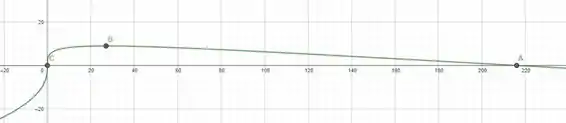
Resposta
Máximo relativo:
Pontos de inflexão:
Concava para cima:
Concava para baixo
O esboço vai ficar:
