Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determina os valores de nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo.
Passo 1
Queremos analisar os possíveis máximos e mínimos da função na reta real toda. Note que se trata de uma função de segundo grau cujo gráfico é uma parábola “feliz”. Sendo assim, sabemos de cara que a função tem um mínimo global e não tem máximo!
Derivando a função com relação a :
Para achar o ponto de mínimo, igualamos a derivada a zero:
Portanto, o mínimo ocorre em
Passo 2
A seguir temos um esboço do gráfico da função:
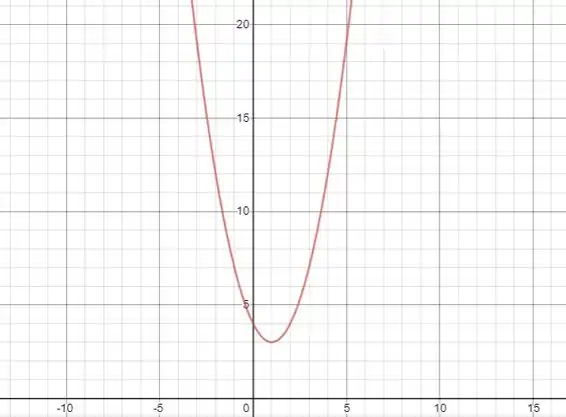
Resposta
Mínimo em . Não tem máximo.