Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.1 - Ex. 42
Ache o valor máximo absoluto e o valor mínimo absoluto da função dada no intervalo indicado pelo método usado nos exemplos 3 e 4 dessa seção. Faça um esboço do gráfico da função no intervalo.
Passo 1
A questão pede para achar os valores máximos e mínimos absolutos da função no intervalo considerado usando o método dos exemplos 3 e 4. Nesses exemplos, usamos o método do intervalo fechado que vale quando o intervalo é fechado e a função é contínua e derivável em todo o intervalo.
O teorema do intervalo fechado garante que sob essas condições, a função terá extremos absolutos (tanto máximo como mínimo) no intervalo. Os candidatos a extremos são os pontos que anulam a derivada e os extremos do intervalo. Basta compararmos os valores da função nesses pontos: o maior será o máximo global e o menor o mínimo!
Vamos derivar para encontrar os pontos críticos:
Assim, fazendo :
Note que ambos os pontos críticos estão no intervalo , de modo que ambos devem ser considerados a extremos absolutos de .
Assim, os candidatos a extremos globais de no intervalo são:
- Pontos críticos: e
- Extremos do intervalo e
Passo 2
Vamos analisar os valores da função nos candidatos a extremos:
Dentre os valores acima, o maior é e o menor é . Assim, é o máximo e é o mínimo.
Passo 3
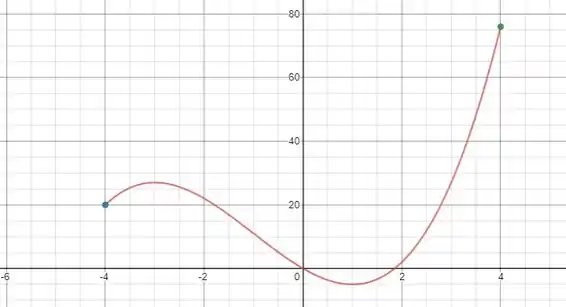
A seguir damos um esboço do gráfico de nesse intervalo:
Resposta
Máximo absoluto: .
Mínimo absoluto: .