Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.1 - Ex. 24
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo.
Passo 1
A questão pede para achar os valores máximos e mínimos absolutos da função no intervalo considerado.
Sabemos que a função é descontínua em . Todavia, note que este ponto não está incluído do intervalo : assim, é contínua e derivável nesse intervalo. Por outro lado, como o intervalo é aberto em uma das extremidades, não podemos aplicar o teorema do valor extremo para garantir que a função tenha extremos globais!
Passo 2
A seguir damos um esboço do gráfico de nesse intervalo:
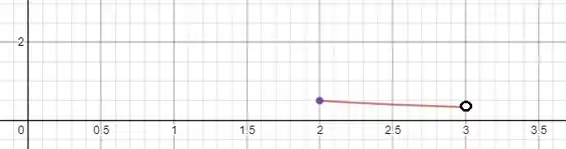
Observe que nesse intervalo, a função é estritamente decrescente, de modo que os extremos absolutos, se existirem, só podem estar nas extremidades do intervalo. Como o intervalo é fechado em e aberto em , temos que é máximo global de , porém ela não apresenta mínimo global no intervalo já que conforme nos aproximamos de o valor da função sempre diminui. Se o intervalo fosse fechado em , então teríamos que seria o mínimo absoluto, porém não é este o caso!
Resposta
Máximo absoluto: .
Mínimo absoluto: não tem.