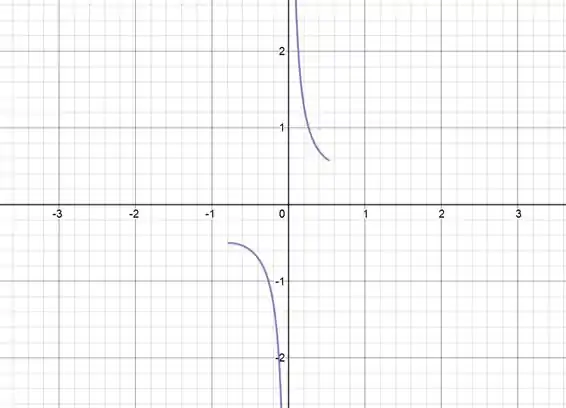
Ache o valor máximo absoluto e o valor mínimo absoluto da função dada no intervalo indicado pelo método usado nos Exemplos 3 e 4 desta secção. Faça um esboço do gráfico da função no intervalo.
Passo 1
Vamos seguir um passo a passo tranquilo pra resolver esses problemas, da mesma forma que o livro faz nos exemplos 3 e 4 desta seção.
- Determinar a derivada da função.
- Fazer e depois encontrar os valores de para os quais não existe.
- Achar os valores de que satisfazem as proposições acima e estão dentro do intervalo especificado.
- Dos valores encontrados, o menor vai ser o mínimo absoluto e o maior será o máximo absoluto do intervalo.
- Esboçar o gráfico utilizando os valores de máximo e mínimo que temos.
Vamo devagarinho que dá bom!
Passo 2
Antes de tudo, vamos relembrar o gráfico da :
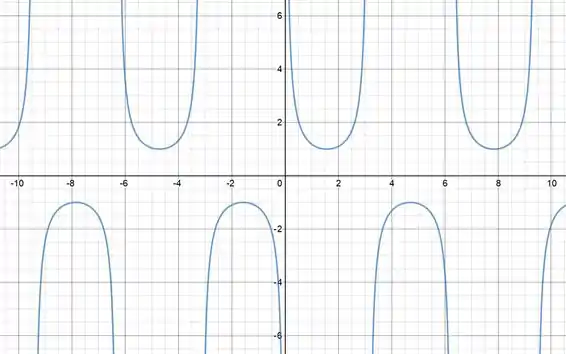
Lembre-se da relação:
Então os pontos que . E também: . Esse é o jeito mais tranquilo de encontrar o gráfico da .
Passo 3
Vamos agora para a derivada da função:
Aplicando a regra da cadeia e lembrando que
Daí temos a derivada da nossa função:
Passo 4
Agora precisamos dos pontos onde a derivada da função não existe ou é igual a . Lembre-se que:
E
Nenhuma das duas funções se igual a em momento algum, maaaas temos pontos onde elas não existem e vamos nos aproveitar deles. Não vamos nos preocupar muito com os pontos onde a não está definida, pois esses pontos também não estarão definidos na nossa função. Vamos à .
Precisamos que:
Então:
Para qualquer inteiro.
Mas no nosso caso temos:
Ou seja, a precisa que:
Logo:
Passo 5
Então precisamos satisfazer a equação acima e o intervalo determinado pela questão também: Podemos ver que o único valor de que satisfaz ambas as condições é Mas não pode ser , porque a não está definida na origem!
Passo 6
E agora? O teorema está errado? Toda a matemática está errada? Calma lá, jovem. Vamos reescrever o teorema aqui:
Se a função for contínua no intervalo fechado , então terá um valor máximo absoluto e um valor mínimo absoluto em .
Agora repare novamente lá em cima no gráfico da cossecante. Encontrou o problema? A cossecante não é contínua! E nosso teorema não garante que tenhamos máximos e mínimos absolutos em intervalos onde a função é descontínua! E como vimos a partir da nossa analise no passo 4, a função não satisfaz nenhuma das condições que impusemos simultaneamente, então podemos afirmar que a função não possui máximo nem mínimo absoluto no intervalo dado. O gráfico dela fica assim:
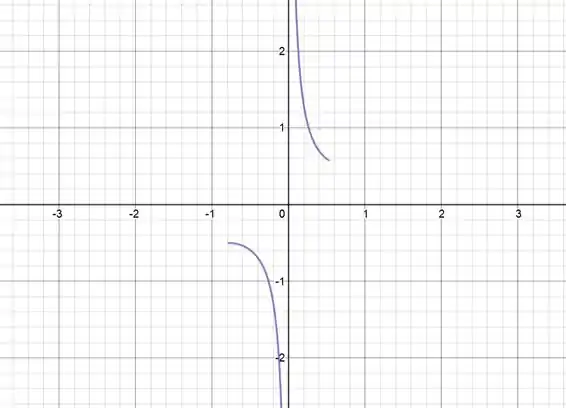
Resposta
Não tem extremos absolutos.