Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.7 - Ex. 18

Ache o valor médio da função f definida por f x = x 2 no intervalo - 1 ,   2 , dado que ∫ - 1 2 x 2 d x = 3 . Ache também o valor de x   no qual ocorre o valor médio. Dê uma interpretação geométrica dos resultados.

Passo 1

O teorema do valor médio para integrais diz que se temos uma função f contínua num intervalo [ a , b ] , vai existir um número χ dentro do intervalo para o qual:

∫ a b f x d x = f ( χ ) ( b - a )

Esse valor f ( χ ) é considerado o valor médio da função no intervalo dado, então achamos o valor médio pela seguinte fórmula:

f χ = ∫ a b f x d x b - a

Passo 2

Aplicando o teorema, achamos f ( χ ) :

f χ = ∫ - 1 2 x 2 d x 2 - - 1 = 3 3 = 1

Então 1 é o valor médio da função f x = x 2 no intervalo [ - 1,2 ] . Como f χ = χ 2 , o valor para o qual o valor médio ocorre é χ = 1 (não pode ser χ = - 1 pois está no extremo do intervalo).

Passo 3

Podemos interpretar geometricamente o resultado mostrando o gráfico de f x = x 2 no intervalo dado e seu valor médio f 1 = 1 . A área abaixo do gráfico de f ( x ) será exatamente a área do retângulo com base indo de - 1,0 e ( 2,0 ) e de altura 1 .

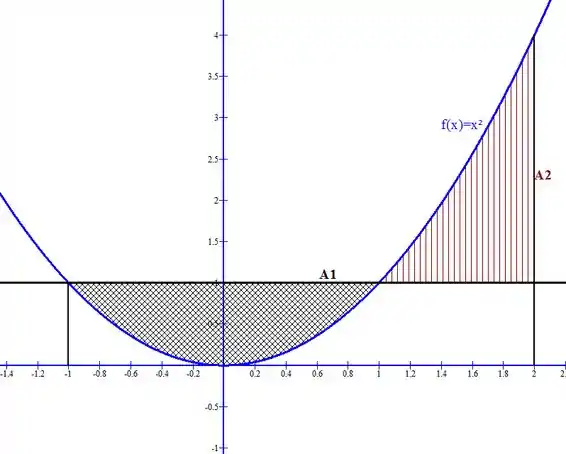
Perceba que, pelo teorema, as áreas A 1 e A 2 são iguais.

Resposta

f 1 = 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o valor de χ que satisfaz o teorema do valor médio para integrais para a integral a seguir. Faça uma figura ilustrando a aplicação do teorema. ∫ 1 2 x 3 = 15 4
Dado que ∫ - 1 2 x d x = 3 2 , ache o valor médio da função identidade no intervalo [ - 1,2 ] . Ache também o valor de x para o qual ocorre o valor médio. Dê uma interpretação geométrica dos resultado
Ache o valor de χ que satisfaz o teorema do valor médio para integrais para a integral a seguir. Faça uma figura ilustrando a aplicação do teorema. ∫ 0 2 x 2 d x = 8 3
Ache o valor de χ que satisfaz o teorema do valor médio para integrais para a integral a seguir. Faça uma figura ilustrando a aplicação do teorema. ∫ - 2 2 ( x 3 + 1 ) = 4
Ache o valor médio da função f definida por f x = sec 2 ⁡ x no intervalo 0 , π 4 , dado que ∫ 0 π / 4 sec 2 ⁡ x d x = 1 . Ache também o valor de x no qual ocorre o valor médio. Dê uma interpretação ge