Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 32
Ache o volume do sólido gerado pela rotação da região limitada pelo gráfico de , pelo eixo y e pela reta 6 em torno da reta .
Passo 1
Vamos colocar as delimitações da região em uma imagem para facilitar:
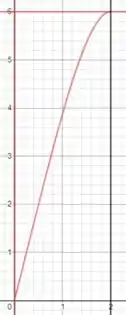
A região entre as três linhas vermelhas é a região que iremos rotacionar e a linha preta é o eixo. Usaremos a equação do volume por invólucro cilíndrico:
Passo 2
Como a região está acima da curva y, para escrevermos f(x) precisaremos subtrair a altura da linha horizontal pela curva :
Como precisamos rotacionar em torno de um eixo que não é o eixo y, precisamos ‘adaptar o integrando da equação do Passo 1, substituiremos x por para que a rotação seja em torno da reta . E os limites de integração serão e , por causa das duas retas, uma de delimitação do eixo y e a outra de rotação. Nossa equação então ficará:
Passo 3
Agora vamos resolver a integral acima, primeiro reescrevendo o integrando:
Integrando cada termo:
Substituindo os limites de integração: