Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 29

Ache o volume do sólido gerado pela rotação da região do Exemplo 2 em torno da reta x = 1 .

Passo 1

No Exemplo 2 a região é dada por y = 3 x - x 3 , pelo eixo y e pela reta y = 2 , como na imagem a seguir:

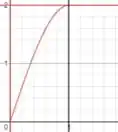
Onde as três linhas vermelhas delimitam a região e a reta preta é o eixo que precisamos rotacionar a região para gerar o sólido. Usando a equação de volume por invólucro cilíndrico:

V = 2 π ∫ a b x f x d x

Passo 2

Como a rotação não é em torno do eixo y, mas sim de um eixo que está uma unidade de distância, precisamos substituir o x na equação por 1 - x para podermos rotacionar em torno do eixo falado no enunciado. Além disso, nossa f(x) será a região acima da curva dada, então precisamos subtrair a curva da altura da reta horizontal:

f x = 2 - 3 x - x 3

E os limites de integração serão x = 0 , por causa da delimitação do eixo y e x = 1 , por causa do eixo de rotação.

Nossa equação então ficará:

V = 2 π ∫ 0 1 1 - x 2 - 3 x - x 3 d x

Passo 3

Reescrevendo a integral acima:

V = 2 π ∫ 0 1 - x 4 + x 3 + 3 x 2 - 5 x + 2 d x

Integrando cada termo:

V = 2 π - 1 5 x 5 + 1 4 x 4 + x 3 - 5 2 x 2 + 2 x 1 0

Substituindo os limites:

V = 2 π - 1 5 + 1 4 + 1 - 5 2 + 2 = 11 π 10

Resposta

V = 11 π 10

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios 31-36, determine os volumes dos sólidos obtidos com a rotação das regiões em torno dos eixos dados. Se preferir, você poderá usar anéis para resolvê-los. 34 – A região no primeiro quadr
41 – Uma conta (de um colar) é feita de uma esfera de raio 5, ao se perfurar diametralmente a esfera usando uma broca de raio 3. B – Determine o volume da porção removida da esfera.
Nos exercícios 31-36, determine os volumes dos sólidos obtidos com a rotação das regiões em torno dos eixos dados. Se preferir, você poderá usar anéis para resolvê-los. 36 – A região limitada por y =
37 – A região no primeiro quadrante limitada em cima pela curva y = 1 x 1 4 a esquerda pela reta x = 1 16 e abaixo da reta y = 1 é girada em torno do eixo x para gerar um sólido. Determine o volume do
38 – A região no primeiro quadrante limitada em cima pela curva y = 1 x a esquerda pela reta x = 1 4 e abaixo da reta y = 1 é girada em torno do eixo y para gerar um sólido. Determine o volume do sóli