De acordo com a Lei de Coulomb, a força F de atração entre duas cargas pontuais positiva e negativa é inversamente proporcional ao quadrado da distância x entre elas
(a) Supondo que a força de atração entre as cargas seja de 0,0005 newton quando a distância entre elas for de 0,3 metro, encontre a constante de proporcionalidade (com unidades apropriadas).
(b) Encontre a força de atração das cargas pontuais quando elas estiverem a 3 metros uma da outra
(c) Faça um gráfico da força versus distância para as duas cargas.
(d) O que acontece com a força se as partículas ficarem cada vez mais perto uma da outra? O que acontece se ficarem cada vez mais longe uma da outra?
Passo 1
(a) Se a força é inversamente proporcional ao quadrado da distância, nós temos essa relação entre elas:
Podemos isolar a constante:
Como temos e :
Passo 2
(b) Aqui, vamos apenas usar a fórmula:
Queremos , se :
Passo 3
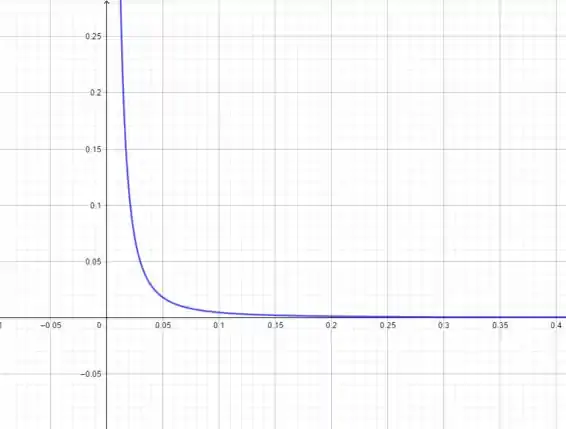
(c) Para fazer o gráfico da força versus distância, vamos plotar a fórmula.
O gráfico fica assim:
Passo 4
(d) Pelo gráfico, a gente pode ver que quanto mais perto as duas partículas estão, mais forte será a força de atração entre elas. O problema é que temos uma assíntota vertical em , pois temos uma divisão por :
E, conforme afastamos as partículas, a força diminui, tendendo a
E isso bate com a proporcionalidade que vimos lá no início: a força é inversamente proporcional ao quadrado da distância.
Resposta
(a)
(b)
(c) 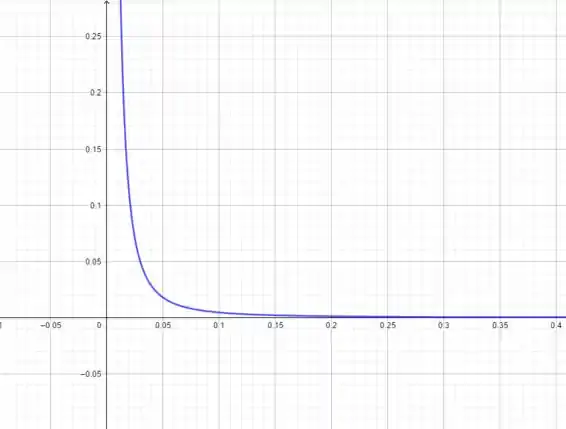
(d) A força aumenta. A força diminui.