Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 - Ex. 15
Encontre a fórmula para
Passo 1
Toda vez que formos inverter uma função galera, vamos seguir três passos, ok? São eles:
Por extenso, temos:
- Passo 1: Escrever a função como igual a uma função de
- Passo 2: Isolar de forma que possamos escrever ele como uma função de
- Passo : Trocar de lugar e chamar a nova função de encontrada da inversa
Bora lá?
Passo 2
Já que a gente tem duas leis de formação, vamos com calma. Pra primeira, temos:
Portanto, pra invertermos esse pedaço, podemos começar subtraindo dos dois lados:
Multiplicando os dois lados por , temos:
Só que temos uma coisa importante pra fazer ainda, considerar que ! Se pegarmos essa inequação e subtrairmos dela unidades dos dois lados, ficamos com
Multiplicando os dois lados por , ficamos com:
Veja que a definição de apareceu do lado esquerdo, logo:
Juntando esses resultados, temos:
E trocando de lugar, a primeira lei de formação se torna:
Bora pra próxima lei de formação!
Passo 3
Vamos repetir essa ideia, ok? Só que agora, pra:
Pra inverter essa função é bem tranquilo. Basta multiplicar os dois lados por :
Como temos:
Ao invertermos, vamos ter:
Mas calma gafanhoto, a gente tem que ter um enorme cuidado aqui. Afinal, em
Está implícito que ! Portanto só responder não é o suficiente! O intervalo correto é:
Po galera, juntando tudo então, temos que, ao isolar , a lei de formação:
Vira:
Então pra achar a inversa desse carinha basta trocar de lugar agora:
Passo 4
Bora juntar os resultados. No passo e , achamos as respectivas inversas:
Portanto, seja:
A nossa inversa será:
E olha que bacana que fica o gráfico das funções:
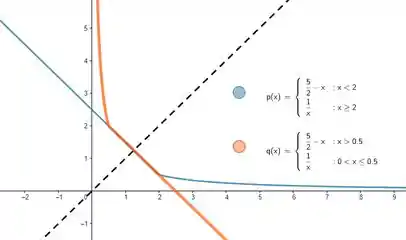
Resposta
blablablablabla