Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.6 - Ex. 6

Associe cada uma das seções cônicas nos Exercícios 5-8 com estas equações:

x 2 4 + y 2 9 = 1 , x 2 2 + y 2 = 1

y 2 4 - x 2 = 1 , x 2 4 - y 2 9 = 1

Em seguida, encontre os focos e vértices da seção cônica. Se a seção cônica for uma hipérbole, encontre também suas assíntotas.

Passo 1

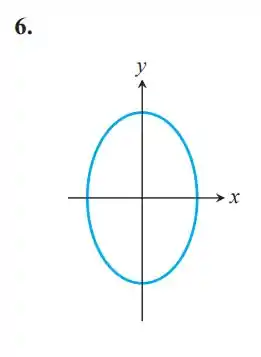
Fala gente tudo bem? Essa figura representa uma elipse vertical, ou seja, o denominador do y é maior que o denominador de x.

Portanto, a única equação que pode ser associada é:

x 2 4 + y 2 9 = 1

Passo 2

Para encontrar os focos da elipse devemos encontrar o ponto c através da fórmula que aprendemos nessa seção.

x 2 a 2 + y 2 b 2 = x 2 4 + y 2 9 = 1

c = b 2 - a 2 = 9 - 4 = 5

Os focos são 0 , ± c = ( 0 , ± 5 ) , pois os focos estão no eixo y.

Os vértices são 0 , ± b = ( 0 , ± 3 )

Bora pro próximo.

Resposta

Os focos são ( 0 , ± 5 ) e os vértices são ( 0 , ± 3 )

Exercícios de Livros Relacionados

Nos Exercícios 17-24, encontre a excentricidade da hipérbole. Em seguida, encontre e desenhe os focos e diretrizes da hipérbole. y 2 - x 2 = 8
Nos Exercícios 1-8, encontre a excentricidade da elipse. Em seguida, encontre e desenhe os focos e diretrizes da elipse. 2 x ²+y ²=2 ² ²
Nos Exercícios 17-24, encontre a excentricidade da hipérbole. Em seguida, encontre e desenhe os focos e diretrizes da hipérbole. 8 y 2 - 2 x 2 = 16
Os Exercícios 13-16 fornecem os focos e as diretrizes correspondentes das elipses centradas na origem do plano xy. Em cada um dos casos, utilize as dimensões na Figura 11.45 para encontrar a excentric
Os Exercícios 25-28 fornecem as excentricidades e os vértices ou focos das hipérboles centradas na origem do plano xy. Em cada um dos casos, encontre a equação de forma padrão da hipérbole nas coorden