Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.4 - Ex. 28
No beisebol, um batedor rebate uma bola, que está acima do chão, em direção à parte central do campo, que tem de altura e dista da base do lançamento. A bola deixa o bastão com uma velocidade escalar de e com ângulo de acima da horizontal. Foi home run? (Em outras palavras, a bola passou por cima da cerca?)
Passo 1
Olá, tudo bem? Para resolver essa questão vamos fazer um desenho e pegar todas as informações que o enunciado trás, assim poderemos visualizar melhor o que está acontecendo.
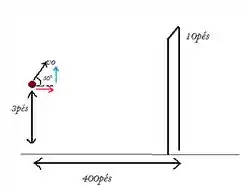
O problema nos diz que a bola tem uma posição inicial e uma velocidade inicial de módulo e ângulo de elevação de .
No desenho o vetor azul representa a velocidade inicial vertical e o vetor vermelho, a horizontal.
A bola é arremessada e descreve uma curva parabólica na direção da cerca e o que queremos saber é, se com as condições iniciais de lançamento, a bola passa acima da cerca.
Os dados iniciais:
- Velocidade inicial:
- Ângulo de elevação:
- Aceleração da gravidade em :
- Vetor posição inicial:
Primeiro vou calcular a velocidade inicial da componente vertical e horizontal da bola.
- Vertical:
- Horizontal:
Para descobrirmos se tivemos um home run ou não, iremos encontrar o período que a bola leva para se deslocar a até a cerca, com esse tempo em mãos, iremos na relação da altura da bola e veremos qual a sua posição nesse tempo, se ela for maior que a altura da cerca, a bola passou, se não for, então a bola não passou e não foi home run.
Passo 2
Agora podemos montar o vetor posição em função do tempo :
Beleza até aqui?
Passo 3
Agora vamos pensar um pouco. O tempo que a bola leva para percorrer, na horizontal, a distância de não é o mesmo tempo que a bola leva subindo? É SIM! Então, da componente horizontal, vamos isolar o tempo :
E agora substituir na componente vertical essa quantidade. Daí vamos encontrar o valor da posição vertical da bola quando chega na cerca e, sabendo disso, podemos aí dizer se foi home run ou não, sacou?
Beleza! Vamos às substituições! Pegando a componente vertical da posição em função do tempo:
E substituindo pelo tempo temos:
E simplificando um pouco teremos:
Agora dá uma espiada no passo e resgata de lá os valores de :
E jogando tudo isso na calculadora vamos ter:
Ou seja, foi sim home run! A bola está acima da cerca (posição vertical) quando passa na posição horizontal de .
Certo? Vamos pra próxima?
Resposta
Foi home run