Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.2 - Ex. 7
7 -
Passo 1
As equações dadas são:
O objetivo é encontrar os pontos críticos para o sistema especificado.
Os pontos críticos são encontrados resolvendo as equações algébricas:
Isso é,
ou
ou
Passo 2
Resolva as equações e e, em seguida, obtenha
Se então .
E quando então .
Da equação , se e , então .
Da equação , se e , então .
Portanto, os pontos críticos são:
Passo 3
b) O campo de direção e o retrato de fase do sistema fornecido são mostrados abaixo:
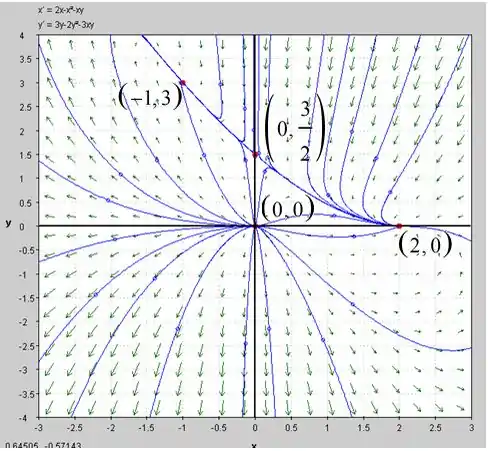
Passo 4
c) O campo de direção que contém o ponto crítico é mostrado abaixo:
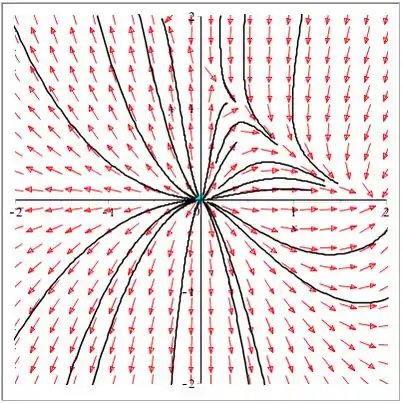
Observe que no retrato da fase acima, todas as curvas se afastam do ponto crítico .
Portanto, o ponto crítico é um nó instável.
Passo 5
O campo de direção que contém o ponto crítico é mostrado abaixo:
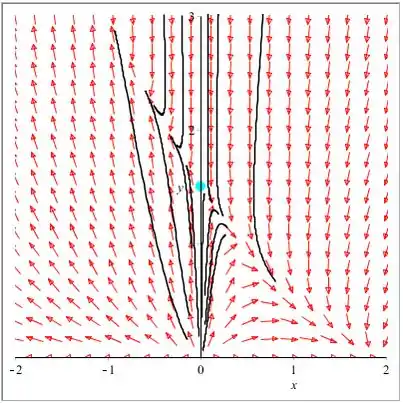
Observe que no retrato da fase acima, todas as curvas se movem em direção ao ponto crítico .
Portanto, o ponto crítico é o ponto de sela e instável.
Passo 6
O campo de direção que contém o ponto crítico é mostrado abaixo:
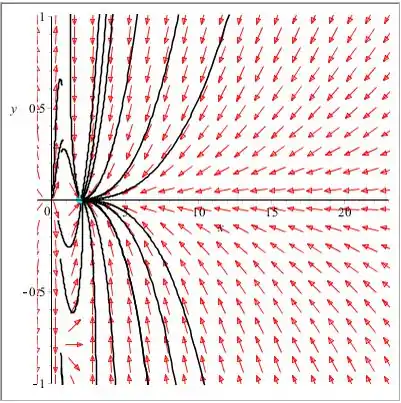
Portanto, o ponto crítico é um nó e assintoticamente estável.
Passo 7
O campo de direção que contém o ponto crítico é mostrado abaixo:
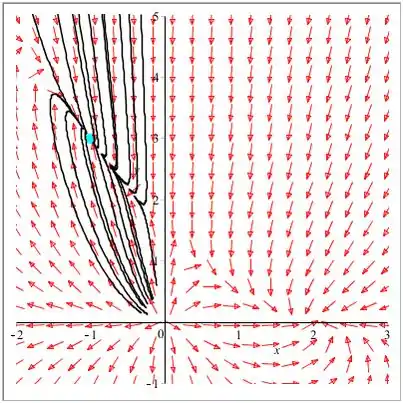
Observe que no retrato da fase acima, todas as curvas se movem em direção ao ponto crítico .
Portanto, o ponto crítico é nó e assintoticamente estável.
Passo 8
d)
O retrato da fase acima mostra que a bacia de atração do ponto crítico é o primeiro, terceiro e quarto quadrante e a bacia de atração do ponto crítico é o segundo quadrante.
Resposta
- Os pontos críticos .
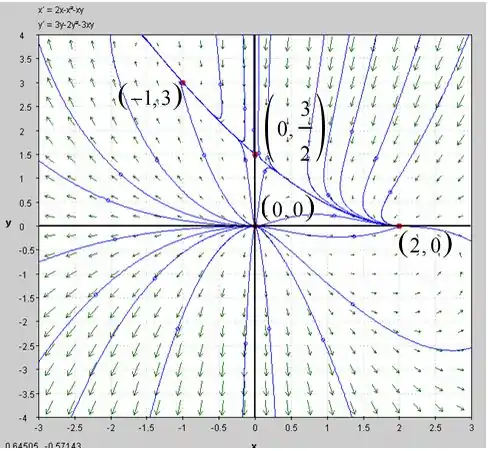
- O ponto crítico é um nó instável.
- O retrato da fase acima mostra que a bacia de atração do ponto crítico é o primeiro, terceiro e quarto quadrante e a bacia de atração do ponto crítico é o segundo quadrante.
O ponto crítico é o ponto de sela e instável.
O ponto crítico é um nó e assintoticamente estável.
O ponto crítico é nó e assintoticamente estável.