Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.2 - Ex. 1
1 -
Passo 1
As equações dadas são:
Considere
Então,
Integrando ambos os lados,
Ou
Onde é uma constante arbitrária de integração.
Forme a condição inicial fornecida.
Então,
Portanto, a solução da equação (1) é
Passo 2
Considere
Então,
Integrando ambos os lados,
Ou
Onde é uma constante arbitrária de integração.
Forme a condição inicial fornecida.
Então,
Portanto, a solução da equação (2) é
Passo 3
Agora,
Ou,
Integrando ambos os lados,
Ou, .
Inicialmente , .
Então
Portanto, as soluções necessárias são:
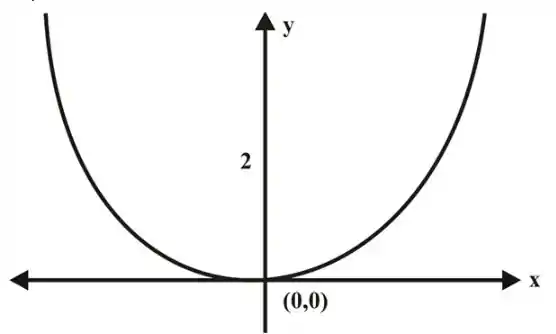
Então a trajetória desse sistema é uma parábola ascendente que passa pela origem e tem foco 2.
Passo 4
A trajetória é dada como:
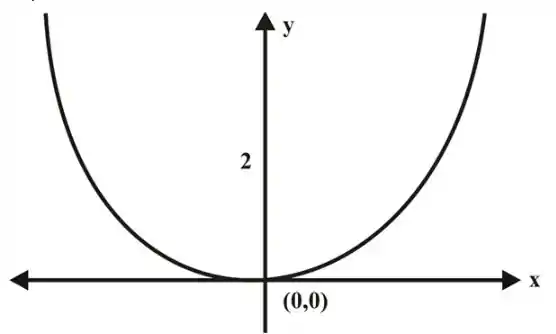
Para determinar a direção do movimento ao longo da trajetória, vemos que, para condições iniciais positivas, aumenta à medida que aumenta.
Resposta
Exercícios de Livros Relacionados
Prove que, se uma trajetória começa em um ponto não crítico do sistema: d x d t =F x ,y , d y d t =G x ,y então não pode atingir um ponto crítico ( x 0 ,y 0 ) em um intervalo de tempo finito.Sugestão:
2 - (d x)/(d t) = - x , (d y)/(d t) = 2 y ; x (0) = 4 , y (0) = 2 e x (0) = 4 , y (0) = 0 .
5 - d x d t = x - x y , d y d t = y + 2 x y
9 - d x d t = y 2 - x - y , d y d t = - x - y - 2 x y