Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.2 - Ex. 5
5 -
Passo 1
As equações dadas são:
O objetivo é encontrar os pontos críticos para o sistema especificado.
Os pontos críticos são encontrados resolvendo as equações algébricas:
Isso é,
e
Uma maneira de satisfazer a primeira equação é escolhendo .
Então a segunda equação se torna:
Mais uma solução pode ser encontrada escolhendo a primeira equação.
Então a segunda equação se torna:
Assim, existem dois pontos críticos e .
Passo 2
b)
O objetivo é esboçar o campo de direção e o retrato de fase do sistema.
Use os comandos MAPLE para obter o campo de direção e o retrato da fase do sistema.
Carregue o pacote com (DEtools) e use o comando DEplot para obter as curvas da solução no campo de direção.
Comandos de entrada do Maple:
> com (DEtools):
> DEplot ([diff (x (t), t) = x (t) -x (t) * y (t), diff (y (t), t) = y (t) + 2 * x (t) * y (t)], {x (t), y (t)}, t = 0..4, [[x (0) = - 1, y (0) = - 1], [x (0) = -0,5, y (0) = - 0,5], [x (0) = - 1, y (0) = 0,2], [x (0) = 0,4, y (0) = 0,4], [x (0 ) = 0,6, y (0) = 0,6], [x (0) = - 0,6, y (0) = 1], [x (0) = - 0,7, y (0) = 1], [x (0 ) = - 0,9, y (0) = 1]], x = -2..2, y = -2..2, setas = médio, tamanho médio = 0,05, cor da linha = azul);
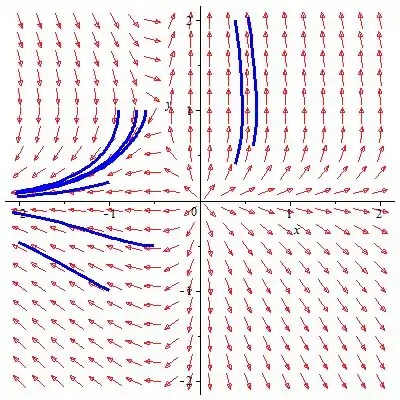
Passo 3
c)
O objetivo é determinar se cada ponto crítico é assintoticamente estável, estável ou instável.
A partir dos retratos da fase acima, observe que todas as trajetórias que começam na origem divergem.
Portanto, o ponto crítico é um nó instável.
Examine as curvas de fase próximas ao ponto crítico da figura, o ponto de equilíbrio tem as propriedades da sela e, portanto, é instável.
Passo 4
d)
O objetivo é descrever a bacia de atração para cada ponto crítico assintoticamente estável.
A partir da figura, observe que não há ponto de equilíbrio assintoticamente estável.
Resposta
a) existem dois pontos críticos e .
b)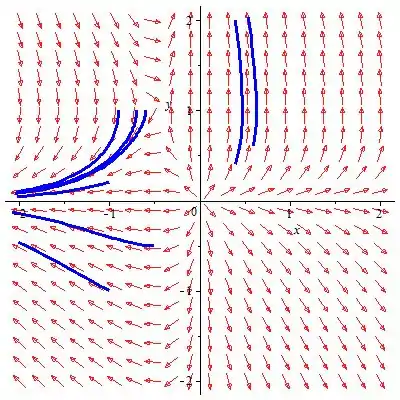 
c) O ponto crítico é um nó instável.
O ponto crítico da figura, o ponto de equilíbrio tem as propriedades da sela e, portanto, é instável.
d)O objetivo é descrever a bacia de atração para cada ponto crítico assintoticamente estável.
A partir da figura, observe que não há ponto de equilíbrio assintoticamente estável.