Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.2 - Ex. 17

17 - (d x)/(d t) = 2 y , (d y)/(d t) = 8 x

Passo 1

  1. As equações dadas são:

(d x)/(d t) = 2 y e (d y)/(d t) = 8 x ... ... . . ( 1 )

(d y)/(d x) = ((d y)/(d t))/((d x)/(d t))

= (8 x)/(2 y)

= (4 x)/(y)

Portanto, a equação diferencial,

(d y)/(d x) = (4 x)/(y)

Passo 2

Separando a varável,

y d y = 4 x d x

Integrando ambos os lados, temos:

int y d y = int 4 x d x

(1)/(2) y^2 = 2 x^2 + c_1

Temos que int u^n d u = (u^(n + 1))/(n + 1) + c

2 x^2 - (y^2)/(2) = - c_1

4 x^2 - y^2 = - 2 c_1

4 x^2 - y^2 = c

Portanto, as soluções necessárias são fornecidas por:

H (x , y) = 4 x^2 - y^2 = c

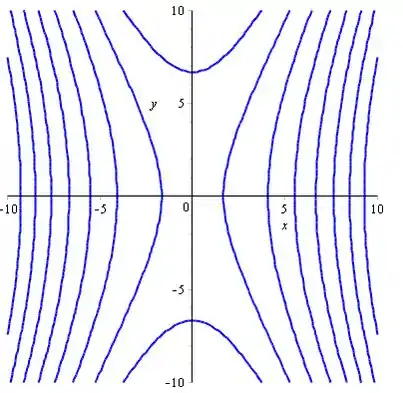
Portanto, as trajetórias são hipérboles.

Passo 3

b)

Use o software Maple para desenhar as curvas de nível da função.

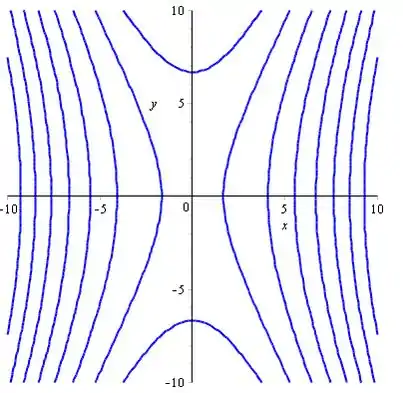
Portanto, a curva de cada nível representa as trajetórias do sistema (1).

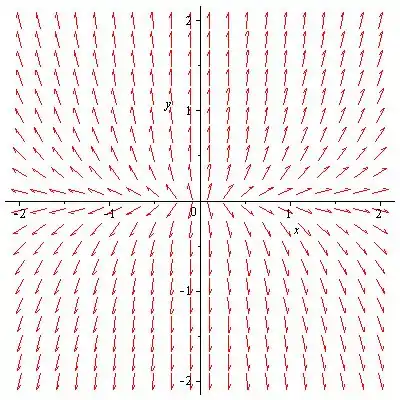
A direção do movimento nas trajetórias pode ser determinada traçando um campo direcional para o sistema (1).

Passo 4

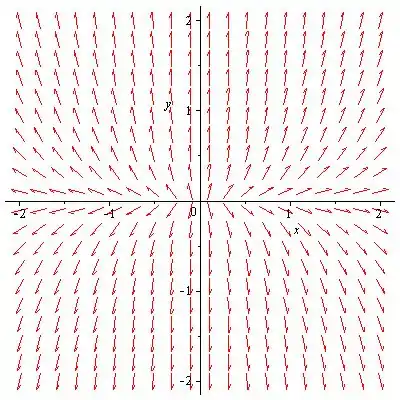
Observe o campo de direção do sistema (1), que representa a direção do movimento nas trajetórias do sistema (1).

Resposta

  1. H (x , y) = 4 x^2 - y^2 = c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

14 - (d x)/(d t) = ( 2 - x ) ( y - x ) , (d y)/(d t) = y ( 2 - x - x^2 )
18 - (d x)/(d t) = 2 y , (d y)/(d t) = - 8 x
16 - (d x)/(d t) = x (2 - x - y) , (d y)/(d t) = ( 1 - y ) ( 2 + x )
15 - (d x)/(d t) = x (2 - x - y) , (d y)/(d t) = - x + 3 y - 2 x y