18 -
Passo 1
- As equações dadas são:
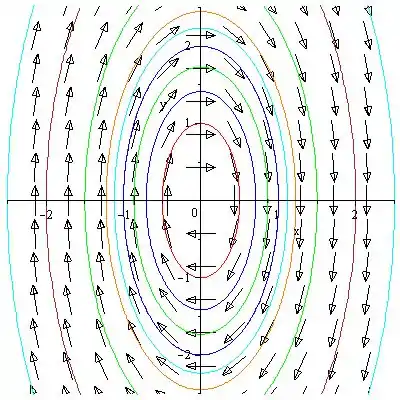
- Gráficos de várias curvas de nível e a direção das trajetórias para diferentes valores de são apresentados abaixo:
Portanto, a equação diferencial,
Passo 2
Separando a varável,
Integrando ambos os lados, temos:
Temos que
Portanto, as soluções necessárias são fornecidas por:
Portanto, as trajetórias são elipses.
Passo 3
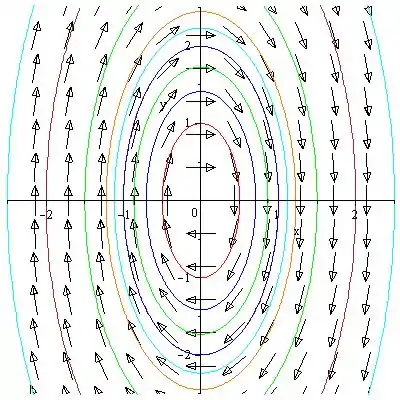
Uma plotagem por computador é útil para exibir as curvas de nível de , algumas das quais são mostradas acima. A direção do movimento nas trajetórias pode ser determinada desenhando um campo de direção para o sistema fornecido. Observe que existe um ponto espiral na origem.
Resposta