Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 65

Cada um dos Exercícios 59-80 fornece a primeira derivada de uma função contínua y = f(x). Determine y" e então use os passos 2-4 do procedimento para construção de gráficos da página 237 para esboçar a forma geral do gráfico de f.

65-

y ' = 8 x - 5 x 2 4 - x 2

Passo 1

Fazendo y’=0 para achar os pontos críticos, temos que:

4 - x = 0 → x = 4

Ou

8 x - 5 x 2 = 0

Nesse caso temos:

x = 0

Ou

x = 8 5

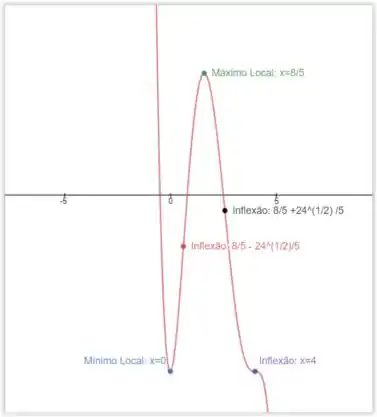
Logo temos os pontos críticos

x = 0 ; x = 4 ; x = 8 5

Passo 2

Derivando y’ para podermos testar esse pontos nós temos:

y ' ' = 8 x - 5 x 2 ' 4 - x 2 + ( 8 x - 5 x 2 ) ( 4 - x 2 ) '

y ' ' = 8 - 10 x 4 - x 2 - 2 ( 4 - x ) ( 8 x - 5 x 2 )

y ' ' = 4 - x [ 8 - 10 x 4 - x - 2 8 x - 5 x 2 ]

y ' ' = ( 4 - x ) ( 20 x 2 - 64 x + 32 )

y ' ' = 4 ( 4 - x ) ( 5 x 2 - 16 x + 8 )

Passo 3

Testando os pontos críticos:

Para x = 0 :

y ' ' 0 = 4 4 - 0 8 → p o s i t i v o

Logo x = 0 representa um ponto de mínimo local

Para x = 4

y ' ' 4 = 4 0 5 × 4 2 - 16 × 4 + 8 → z e r o

Não podemos dizer nada sobre x = 4

Para x = 8 5

y ' ' 8 5 = 4 4 - 8 5 5 × 8 5 2 - 16 × 8 5 + 8 = 4 × 2.4 × - 4.8 → n e g a t i v o

Logo x = 8 5

Representa um ponto de máximo local.

Pontos de inflexão:

4 - x = 0 → x = 4

5 x 2 - 16 x + 8 = 0

Valores de x iguais a: x = 8 5 ± 24 5

Passo 4

Organizando os intervalos temos:

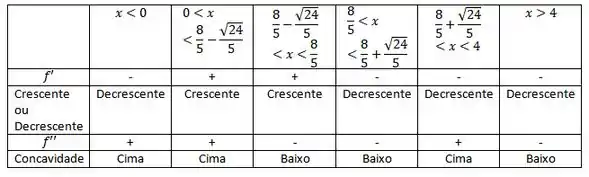
Logo x=4 é um ponto de inflexão.

Resposta

y ' ' = 4 ( 4 - x ) ( 5 x 2 - 16 x + 8 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nestes exercícios, dê as respostas com tantas casas decimais quantas forem permitidas por seu recurso computacional, mas siga o procedimento delineado na caixa Domínio da Tecnologia à página 298 .Use
Se o gráfico de f tiver uma cúspide em x = 1 , então f não pode ter uma inflexão em x = 1 .
Suponha que o gráfico de uma função f tenha sido obtido com um recurso computacional. Discuta a informação que as técnicas do Cálculo podem fornecer a respeito de f além do que pode ser deduzido do gr
A figura Ex-70 mostra o gráfico do polinômio y = 0,1 x 5 x + 1 2 gerado em um computador usando uma janela de - 2 ; 1,5 × 0,2 ; 0,2 . Mostre que a escolha da janela vertical faz com que o computador p
A figura Ex-69 mostra o gráfico do polinômio y = 0,1 x 5 x - 1 gerado em um computador usando uma janela de - 2 ; 2,5 × - 1 ,5 . Mostre que a escolha da escala vertical faz com que o computador perca