Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 72
Suponha que o gráfico de uma função tenha sido obtido com um recurso computacional. Discuta a informação que as técnicas do Cálculo podem fornecer a respeito de além do que pode ser deduzido do gráfico exibido na imagem do recurso computacional.
Passo 1
Então galera, para discutirmos sobre isso, nada melhor do que pegarmos um exemplo já resolvido aqui na plataforma. O exercício 70 nos cede o seguinte gráfico:
Que foi plotado com uma janela específica. Mexendo na janela do gráfico, ou seja, alterando a escala do gráfico, chegamos ao seguinte resultado:
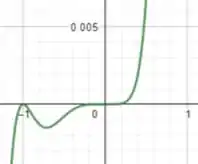
Sim, é o mesmo gráfico!
Passo 2
As informações de uma função só são 100% conhecidas a partir do momento em que calculamos e encontramos seus máximos, mínimos e inflexões. Caso a nossa função não apresente nada de interessante em um intervalo dado, não interfere em nada a escala escolhida. No entanto, se calcularmos os máximos e mínimos, assim como os pontos críticos e se encontrarmos pontos interessantes, então alterar a escala parece viável, tudo dependeria da questão.
Em resumo, apenas as técnicas do Cálculo nos permite enxergar as minúcias de uma função. Sendo assim, o que devemos fazer é analisar com calma o tipo de função que estamos analisando para não cometer um erro grosseiro na análise!
😉
Resposta
Ei, a resposta está no passo a passo :)