Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.5 - Ex. 61b
Um peso está ligado a uma mola e atinge a sua posição de equilíbrio . Em seguida, ele é posto em movimento, o que resulta em um deslocamento de
Em que é medido em centímetros e é medido em segundos. Veja a figura a seguir.
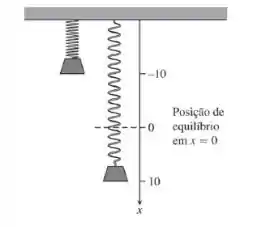
- Determine o deslocamento da mola quando , e .
- Determine a velocidade da mola quando , e .
Passo 1
Para determinarmos a posição da mola em cada tempo, precisamos substituir o valor de na equação de posição da mola. Como a equação da posição já nos foi dada, podemos fazer uma substituição direta para obter as posições.
Já para calcular a velocidade, temos que descobrir a sua função anteriormente. Para isto, basta lembrar da física que, dada a função de posição , a velocidade pode ser obtida por:
Portanto, basta derivarmos a função posição. Após obtermos a função velocidade, basta substituirmos os valores de nela para obter a velocidade em cada tempo dado.
Passo 2
Precisamos determinar a função velocidade. Para isto, vamos derivar a função posição. Logo, temos:
Passo 3
Vamos calcular as posições para cada tempo separadamente. Para , temos:
Passo 4
Para , temos:
Passo 5
Para , temos:
Resposta
Para , .
Para , .
Para , .