Cada um dos gráficos dos Exercícios 25 e 26 é o gráfico da função posição de um corpo que se desloca ao longo de um eixo coordenado (t representa o tempo). Em que tempo aproximadamente, se houver, cada corpo tem (a) velocidade igual a zero? (b) aceleração igual a zero? Durante aproximadamente que intervalos de tempo o corpo se move (c) para a frente? (d) para trás?
25.
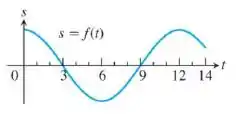
Passo 1
a.
A velocidade é a derivada do posição em relação ao tempo, ou seja, quando a derivada desse gráfico for igual a zero a velocidade será nula. Podemos observar que isso acontece em e
Passo 2
b.
Sabemos também que a segunda derivada do espaço em relação ao tempo é a aceleração, então a aceleração será nula nos pontos de inflexão, onde a segunda derivada assume valor zero. Esses pontos são: e
Passo 3
c.
Olhando para o gráfico vemos que a posição do corpo vai aumentando de até , ou seja nesse intervalo de tempo o corpo se move para frente.
d.
Também podemos perceber que a posição do corpo vai diminuindo de até e de até , ou seja, nesses intervalos de tempo o corpo se move para trás.
Resposta
a. e
b. até
c.
d. e