Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.3 - Ex. 30
Cada integral representa o volume de um sólido. Descreva o sólido.
Passo 1
Como nossa integral é calculada em temos por padrão que pelo método das cascas o volume de um sólido é dado por
Onde e representam os valores aos quais nossa variável, no caso o , está contida. Dessa forma, vemos que os valores da nossa função estão limitados entre e , assim, devemos ter que a reta está limitando superiormente nossa função e assim nossa região que vai girar em torno do eixo pode ser descrita como
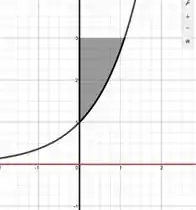
Assim, nosso sólido vai ser dado por essa região destacada girando em torno do eixo .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Nos exercícios 31-36, determine os volumes dos sólidos obtidos com a rotação das regiões em torno dos eixos dados. Se preferir, você poderá usar anéis para resolvê-los. 36 – A região limitada por y =
Nos exercícios 31-36, determine os volumes dos sólidos obtidos com a rotação das regiões em torno dos eixos dados. Se preferir, você poderá usar anéis para resolvê-los. 35 – A região limitada por y =
Nos exercícios 31-36, determine os volumes dos sólidos obtidos com a rotação das regiões em torno dos eixos dados. Se preferir, você poderá usar anéis para resolvê-los. 35 – A região limitada por y =
8 - Determine o volume do sólido gerado pela rotação da região "triangular" limitada pela curva y= 4 x 3 e pelas retas x = 1 e y= 1 2 em torno:Do eixo xDo eixo yDa reta x = 2Da reta y = 4
8 - Determine o volume do sólido gerado pela rotação da região "triangular" limitada pela curva y= 4 x 3 e pelas retas x = 1 e y= 1 2 em torno:Do eixo xDo eixo yDa reta x = 2Da reta y = 4