Investigue a família das curvas dadas por . Em particular, encontre os limites quando e determine os valores e para os quais tem um mínimo absoluto. O que acontece aos mínimos quando cresce?
Passo 1
Temos que , encontrando os pontos críticos
Logo, para que haja ponto crítico e possível máximo e mínimo, . Já , ou seja, f é côncava para cima para qualquer valor real .
Vamos analisar os limites,
Como constante.
O que significa que
Para que as contas dependam de , ou seja,
Temos que
Se e
Se e
Então tem um mínimo absoluto em . Com é crescente então o mínimo esta em e cada vez mais longe da origem.
Passo 2
Vamos usar o software geogebra. Na janela de álgebra vamos por a função e plotar o gráfico de e verificar nossas contas.
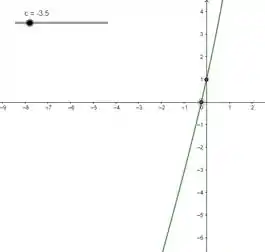
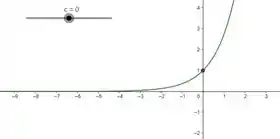
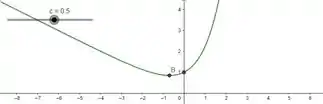
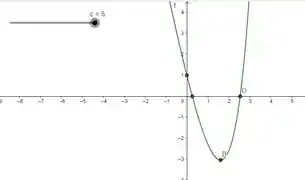
Resposta
Ei, a resposta está no passo a passo :)