Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.8 - Ex. 1f
Em cada parte, determine se a integral é imprópria e, se for, explique por quê.
Passo 1
Faaala aí, pessoal! Prontos pra mais um exercício com o Responde Aí?
Bom, para esse exercício em questão, a ideia é bem simples. Olhando a integral definida dada, precisamos ver se algum valor dentro do intervalo de integração torna o nosso integrando indefinido, ou seja, se a função do integrando não existe pra algum desses valores.
Então, concluímos nessa parte que junto com a ideia de integral, temos a análise de funções.
A resposta terá duas possibilidades: se o nosso integrando não estiver definido em um ponto dentro do intervalo de integração, nossa integral será dita imprópria. Caso contrário, ela não será imprópria e, sim, apenas definida.
Passo 2
Então, para a nossa respectiva integral o integrando é
Dentro do intervalo .
Passo 3
Lembrando que a função tangente tem a seguinte forma:
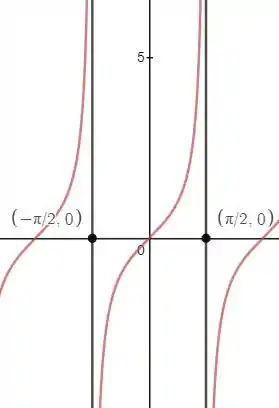
Ela é contínua para valores dentro do intervalo .
Assim, como todos os pontos do nosso intervalo de integração estão contidos no intervalo em que o integrando é contínuo, não apresentando nenhuma descontinuidade, então a integral não é imprópria.
Resposta
Não é imprópria