Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 2
Em cada parte, esboce o gráfico de uma função com as propriedades indicadas.
- é crescente em , tem um ponto de inflexão na origem e é côncava para cima em .
- f é crescente em , tem um ponto de inflexão na origem e é côncava para baixo em .
- f é decrescente em , tem um ponto de inflexão na origem e é côncava para cima em .
- f é decrescente em, tem um ponto de inflexão na origem e é côncava para baixo em .
Passo 1
- Vamos lá, vamos esboçar a função de :
- Vamos agora esboçar o gráfico de :
- Agora vamos esboçar o gráfico de :
- E por último vamos esboçar o gráfico de :
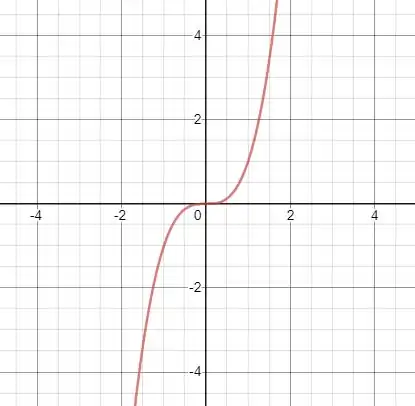
Nela vemos que tem um ponto de inflexão da origem, pois aí muda de concavidade, de côncava para baixo para côncava para cima. E quando a função tende pra infinito positivo e negativo a função é crescente.
Passo 2
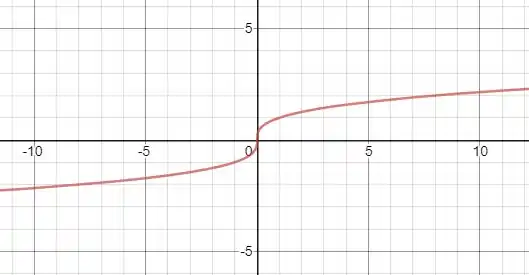
Nela vemos que tem um ponto de inflexão da origem, pois aí muda de concavidade, de côncava para cima para côncava para baixo. E quando a função tende pra infinito positivo e negativo a função é crescente.
Passo 3
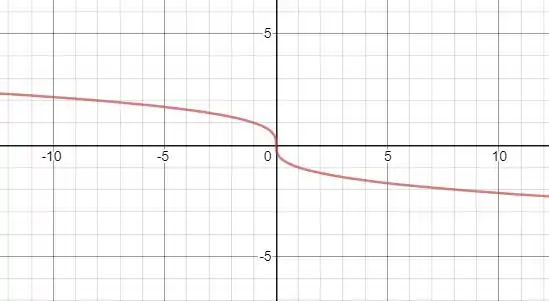
Nela vemos que tem um ponto de inflexão da origem, pois aí muda de concavidade, de côncava para baixo para côncava para cima. E quando a função tende pra infinito positivo e negativo a função é decrescente.
Passo 4
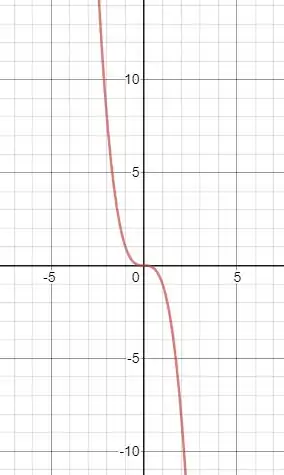
Nela vemos que tem um ponto de inflexão da origem, pois aí muda de concavidade, de côncava para cima para côncava para baixo. E quando a função tende pra infinito positivo e negativo a função é decrescente.
Resposta
Ei, a resposta está no passo a passo :)