Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.4 - Ex. 2c

Para cada ponto crítico, encontre o sistema linear correspondente. Encontre os autovalores e autovetores do sistema linear; classifique cada ponto crítico em relação ao tipo e determine se é assintoticamente estável, estável ou instável.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos e classificarmos os pontos críticos das nossas equações. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser montar o Jacobiano do nosso cmapo vetorial.

J =   1,5 - 2 x - 0,5 y - 0,5 x - 1,5 y 2 - 1,5 x - y

Para os valores iguais a zero, temos os seguintes valores críticos:

x ( 1,5 - x - 0,5 y ) = 0

y 2 - 0,5   y - 1,5 x = 0

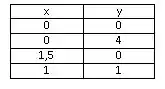
Passo 3

Pronto!! Agora é só substituir esses valores no Jacobiano e achar os autovalores e autovetores!!

J 0   ,   0 =   3 2 0 0 2     ∴       r 1 = 3 2   ; r 2 = 2     ∴       ξ 1 = 1 0   ;   ξ 2 = 0 1   → i n s t á v e l

J 0   ,   4 =   - 1 2 0 - 6 - 2     ∴       r 1 = - 1 2   ; r 2 = - 2     ∴       ξ 1 = 1 - 4   ;   ξ 2 = 0 1   → a s s i n t o t i c a m e n t e   e s t á v e l

J 3 2   ,   0 =   - 3 2 - 3 4 0 - 1 4     ∴       r 1 = - 3 2   ; r 2 = - 1 4     ∴       ξ 1 = 1 0   ;   ξ 2 = 3 - 5   → a s s i n t o t i c a m e n t e   e s t á v e l

J 1   ,   1 = - 1 - 1 2 - 3 2 - 1 2       ∴       r 1 = - 3 + 13 4   ; r 2 = - 3 - 13 4     ∴       ξ 1 = 1 - 1 + 13 2   ;   ξ 2 = 0 - 1 + 13 2   → i n s t á v e l

Resposta

J 0   ,   0 =   3 2 0 0 2     ∴       r 1 = 3 2   ; r 2 = 2     ∴       ξ 1 = 1 0   ;   ξ 2 = 0 1   → i n s t á v e l

J 0   ,   4 =   - 1 2 0 - 6 - 2     ∴       r 1 = - 1 2   ; r 2 = - 2     ∴       ξ 1 = 1 - 4   ;   ξ 2 = 0 1   → a s s i n t o t i c a m e n t e   e s t á v e l

J 3 2   ,   0 =   - 3 2 - 3 4 0 - 1 4     ∴       r 1 = - 3 2   ; r 2 = - 1 4     ∴       ξ 1 = 1 0   ;   ξ 2 = 3 - 5   → a s s i n t o t i c a m e n t e   e s t á v e l

J 1   ,   1 = - 1 - 1 2 - 3 2 - 1 2       ∴       r 1 = - 3 + 13 4   ; r 2 = - 3 - 13 4     ∴       ξ 1 = 1 - 1 + 13 2   ;   ξ 2 = 0 - 1 + 13 2   → i n s t á v e l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja α = 2. Classifique cada ponto crítico investigando o sistema linear correspondente. Desenhe um retrato de fase em um retângulo contendo os pontos críticos..
Seja α = 2. Classifique cada ponto crítico investigando o sistema linear correspondente. Desenhe um retrato de fase em um retângulo contendo os pontos críticos..
Encontre o ponto de bifurcação α0 no qual os pontos críticos coincidem. Localize esse ponto crítico e encontre os autovalores do sistema linear aproximado. Desenhe um retrato de fase..
Para αα0 não existem pontos críticos. Escolha um desses valores de α e desenhe um retrato de fase..
Encontre o ponto de bifurcação α0 no qual os pontos críticos coincidem. Localize esse ponto crítico e encontre os autovalores do sistema linear aproximado. Desenhe um retrato de fase..