Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 11.1 - Ex. 7
Em cada um dos problemas de 7 a 10, suponha que todos os autovalores são reais.
(a) Determine a forma das autofunções e a equação satisfeita pelos autovalores não nulos.
(b) Determine se é um autovalor.
(c) Encontre valores aproximados para e , os dois autovalores não nulos de menor módulo.
(d) Estime para valores grandes de n.
Passo 1
A equação característica da equação diferencial será igual a:
Onde são os autovalores da função. A solução será igual a:
E a equação de será:
Isso considerando que
Passo 2
Considerando que nós teremos:
Integrando duas vezes a equação nós temos que:
E que será:
Então se aplicando a condição de contorno temos que:
E :
Isso é, só teremos a solução trivial, portanto não é um autovalor. Pois o autovalor tem uma solução não trivial.
Passo 3
Aplicando a primeira condição de contorno (na equação encontrada no passo 1) vemos que:
Aplicando agora a segunda condição de contorno (sabendo que )
E sabendo que então o termo será igual a:
E como nós podemos dizer que a autofunção será dada por:
Passo 4
Para fazer a letra nós precisamos plotar os gráficos de:
E de
E comparar quando os dois gráficos se igualam
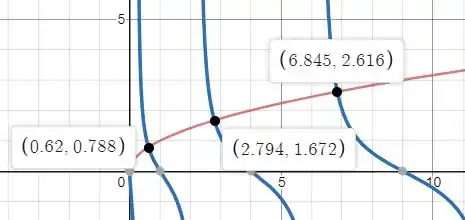
E os dois primeiros (valores na horizontal) estão em:
Passo 5
Outros valores de podem ser dados por:
Ignorando os decimais é como se tivéssemos a sequência:
E uma boa aproximação para essa sequência será:
Para
Essa sequência tem muito a ver com o exemplo desse capítulo.
Resposta
;