Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.8 - Ex. 11

Em cada um dos Problemas 11 e 12:

(a) Encontre a solução do problema de valor inicial dado.

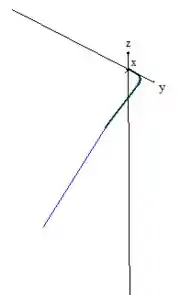
(b) Desenhe a trajetória correspondente no espaço x 1 x 2 x 3 e desenhe, também, o gráfico de x 1 em função de t .

11.

X ' = 1 0 0 - 4 1 0 3 6 2 X ,             X 0 = - 1 2 - 30

Passo 1

L e t r a   A :

Bem, queremos aqui resolver um sistema 3x3. Basicamente a forma de resolução é a mesma dos sistemas 2x2, porém com um cálculo mais chatinho! Mas não se preocupe que vamos destrinchar juntos esses cálculos! Bora?

Primeira coisa é montar a matriz dos coeficientes A baseado no sistema:

A = 1 0 0 - 4 1 0 3 6 2

Agora devemos buscar os autovalores dela!

Passo 2

AUTOVALORES:

Os autovalores λ de uma matriz são do tipo:

det ⁡ A - λ I = 0

Onde basicamente o que devemos fazer é subtrair λ na diagonal principal da matriz A , veja:

det ⁡ 1 - λ 0 0 - 4 1 - λ 0 3 6 2 - λ = 0

O determinante de matriz 3x3 é um pouco mais chato que o 2x2. Aqui você tem que repetir as duas primeiras colunas e fazer aquele esquema de multiplicação de diagonais, se lembra?

  ⁡ 1 - λ 0 0 - 4 1 - λ 0 3 6 2 - λ - λ 1   0 - 2 - λ   1 - 2   = 0     →

1 - λ 2 2 - λ = 0

Então, se a solução dessa equação é um desses 3 valores aqui:

λ 1 = 1 ,             λ 2 = 1                 e               λ 3 = 2

O conjunto de soluções fundamentais x k para cada um deles vão ser:

  • Para o λ 1 que é real e o primeiro a ser analisado...

    • x 1 = v 1 e λ 1 t

  • Para λ 2 que é real e o segundo a ser analisado...

    • x 2 = v 1 t e λ 1 t + v 2 e λ 2 t

  • Para o λ 3 que é real e único:

x 3 = v 3 e λ 3 t

Onde v 1 , v 2 e v 3 são os autovetores determinados por:

A - λ 1 I v 1 = 0

A - λ 2 I v 2 = v 1

A - λ 3 I v 3 = 0

Partiu calcular esses autovetores agora?

Passo 3

AUTOVETOR 1:

A - λ 1 I v 1 = 0

Se chamarmos as coordenadas desse vetor v de:

a b c

Onde a , b e c são os valores das coordenada dele, se os conhecermos então a gente conhece o autovetor! Substituindo ele no lugar de v :

A - λ 1 I a b c = 0

Lembre-se de que menos λ I nada mais é do que subtrair λ da diagonal principal:

1 - λ 1 0 0 - 4 1 - λ 1 0 3 6 2 - λ 1 a b c = 0

Como λ 1 = 1 ...

0 0 0 - 4 0 0 3 6 1 a b c = 0

Resolvendo esse produto matricial aí...

0 = 0 - 4 a = 0 3 a + 6 b + c = 0

Das duas últimas equações...

a = 0

Então...

3 a + 6 b + c = 0     →

c = - 6 b

Se escolhermos b = 1 , então a = 0 e b = - 6 também. Logo, o autovetor associado a esse autovalor é:

v 1 = 0 - 6 1

Passo 4

AUTOVETOR 2:

A - λ 2 I v 2 = v 1

Se chamarmos as coordenadas desse vetor v de:

a b c

Novamente teremos...

A - λ 2 I a b c = 0 1 1

Lembre-se de que menos λ I nada mais é do que subtrair λ da diagonal principal:

1 - λ 2 0 0 - 4 1 - λ 2 0 3 6 2 - λ 2 a b c = 0 - 6 1

Como λ 2 = 1 ...

0 0 0 - 4 0 0 3 6 1 a b c = 0 - 6 1

Resolvendo esse produto matricial aí...

0 = 0 - 4 a = 1 3 a + 6 b + c = 1

Das duas últimas equações...

a = - 1 4     →

3 - 1 4 + 6 b + c = 1       →

6 b + c = 1 + 3 4     →

c = 7 4 - 6 b

Se escolhermos b = 0 e c = 7 4 . Logo, o autovetor associado a esse autovalor é:

v 2 = - 1 4 0 7 4

Passo 5

AUTOVETOR 3:

A - λ 3 I v 3 = 0

Se chamarmos as coordenadas desse vetor v de:

a b c

Novamente teremos...

A - λ 3 I a b c = 0 0 0

Lembre-se de que menos λ I nada mais é do que subtrair λ da diagonal principal:

1 - λ 3 0 0 - 4 1 - λ 3 0 3 6 2 - λ 3 a b c = 0 0 0

Como λ 2 = 2 ...

- 1 0 0 - 4 - 1 0 3 6 0 a b c = 0 0 0

Resolvendo esse produto matricial aí...

- a = 0 - 4 a - b = 0 3 a + 6 b = 0

Da primeira equação...

a = 0    

Da segunda ou terceira...

3 a + 6 b = 0     →             6 b = 0   →

b = 0

Como o c está livre pra ser quem ele quiser (de menos o 0 ) se escolhermos c = 1 esse autovalor é:

v 2 = 0 0 1

Passo 6

Logo, as três soluções fundamentais serão:

x 1 = v 1 e λ 1 t

x 2 = v 1 t e λ 1 t + v 2 e λ 2 t

x 3 = v 3 e λ 3 t

Substituindo...

x 1 = 0 - 6 1 e t

x 2 = 0 - 6 1 t e t + - 1 4 0 7 4 e t

x 3 = 0 0 1 e 2 t

A solução final é então dada pela expressão:

x y z = c 1 x 1 + c 2 x 2 + c 3 x 3   →

x y z = c 1 0 - 6 1 e t + c 2 0 - 6 1 t e t + c 2 - 1 4 0 7 4 e t + c 3 0 0 1 e 2 t  

Ou ainda em notação de chaves, a solução será...

x = - 1 4 e t y = - 6 c 1 e t - 6 c 2 t e t z = c 1 e t + c 2 t e t + 7 4 c 2 e t + c 3 e 2 t

Passo 7

Com a solução em mãos, podemos partir para a busca da solução particular usando a informação de valor inicial:

X 0 = - 1 2 - 30

Desse vetor, tiramos que...

x 0 = - 1

y 0 = 2

z 0 = - 30

Substituindo então o t por 0 na nossa solução...

x = - 1 4 c 2 e t y = - 6 c 1 e t - 6 c 2 t e t z = c 1 e t + c 2 t e t + 7 4 c 2 e t + c 3 e 2 t   →

x 0 = - 1 4 c 2 e 0 y 0 = - 6 c 1 e 0 - 6 c 2 0 e 0 z 0 = c 1 e 0 + c 2 0 e 0 + 7 4 c 2 e 0 + c 3 e 0     →

- 1 = - 1 4 c 2 2 = - 6 c 1 - 30 = c 1 + 7 4 c 2 + c 3     →

Desse sistema, tiramos das duas primeiras equações que...

c 2 = 4

c 1 = - 1 3

Usando esses valores na última equação...

- 30 = c 1 + 7 4 c 2 + c 3   →

- 30 = - 1 3 + 7 + c 3       →

c 3 = - 37 + 1 3         →

- 110 3

Logo, as nossas soluções usando essas constantes...

x = - e t y = 2 e t - 24 t e t z = - 1 3 e t + 4 t e t + 7 e t - 110 3 e 2 t   →

x = - e t y = 2 e t - 24 t e t z = 20 3 e t + 4 t e t - 110 3 e 2 t  

Passo 8

L e t r a   B :

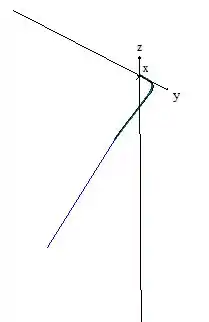
Usando algum aplicativo de plotagem de gráficos (por exemplo, o winplot), podemos plotar o gráfico de y × x × z implicitamente em funções de t :

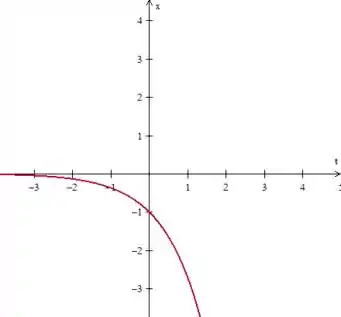
E para o gráfico de x em função de t ...

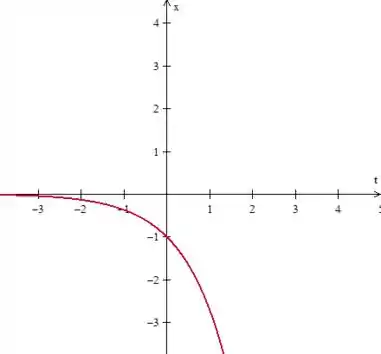
Resposta

Letra A:

x = - e t y = 2 e t - 24 t e t z = 20 3 e t + 4 t e t - 110 3 e 2 t

Letra B:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 15 a 18 , resolva o problema de valor inicial dado. Descreva o comportamento da solução quando t → ∞ x ' = 5 - 1 3 1 x,x 0 = 2 - 1
Considere o sistema com duas massas e três molas cujas equações de movimento são as Eqs.(22) no texto. Suponha que m 1=m 2=1 ,k 1=k 2=k 3=1 .(a) Como no texto, transforme o sistema em quatro equações
Em cada um dos Problemas 11 e 12:(a) Encontre a solução do problema de valor inicial dado.(b) Desenhe a trajetória correspondente no espaço x 1 x 2 x 3 e desenhe, também, o gráfico de x 1 em função de
Em cada um dos problemas de 7 a 10:(a) Encontre a solução do problema de valor inicial dado.(b) Desenhe a trajetória da solução no plano x 1 x 2 e desenhe, também, o gráfico de x 1 em função de t .9.