Considere o sistema com duas massas e três molas cujas equações de movimento são as Eqs.
(22) no texto. Suponha que .
(a) Como no texto, transforme o sistema em quatro equações de primeira ordem da forma Determine a matriz de coeficientes .
(b) Encontre os autovalores e autovetores de .
(c) Escreva a solução geral do sistema.
(d) Descreva os modos fundamentais de vibração. Para cada modo fundamental, desenhe
gráficos de y1 e de y2 em função de t. Desenhe, também, as trajetórias correspondentes nos
planos e .
(e) Considere as condições iniciais . Calcule as constantes arbitrárias na
solução geral do item (c). Desenhe gráficos de y1 e de y2 em função de t. Você acha que a
solução é periódica? Desenhe, também, as trajetórias correspondentes nos planos e .
(f) Considere outras condições iniciais de sua escolha e desenhe gráficos semelhantes aos
pedidos no item (e).
Passo 1
d)
Recomendo fortemente que você abra o item (c) desta questão para acompanha visualmente todas a citações que estamos fazendo durante está questão.
Todas as fases do nosso sistema possui quatro dimensões, e cada solução, obtemos a parcela particular dos valores para na equação da solução geral, que corresponde a trajetória do espaço.
Nós podemos mostrar que as projeções de certas trajetórias no plano , assim podemos mostrar separadamente cada movimento.
Os dois primeiros termos do lado direito da solução geral do sistema está movimentando com uma frequência de 1 a de período. Note que e nestes termos temos também que . Se nós focarmos a solução e plotarmos versus e versus no mesmo eixos, nós iriamos obter os mesma consignação de gráficos de amplitude 1.
A trajetória da primeira massa no plano e segunda massa no plano será igual e mesma posição no circulo de raio 1 atravessando o sentindo anti-horário e começando no ponto e completando o circuito no período ou tempo . A origem é o centro do planos e .
Podemos ter gráficos similares que obtivemos da função ou tendo a mesma combinação linear de e .
Temos também que os termo do lado direito da solução geral que temos, estes termos estão referentes a frequência e o período .
Observe que neste caso, temos e
Passo 2
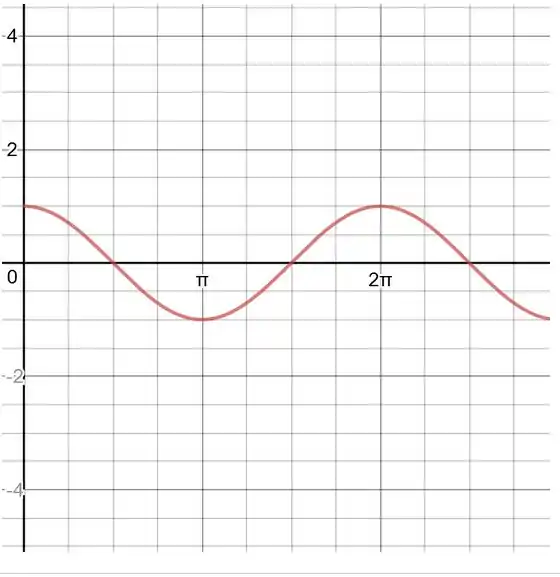
Após toda essa explanação vamos aos gráficos que citamos, primeiramente desenhando o gráfico de versus e versus . Note que eles são iguais:
Passo 3
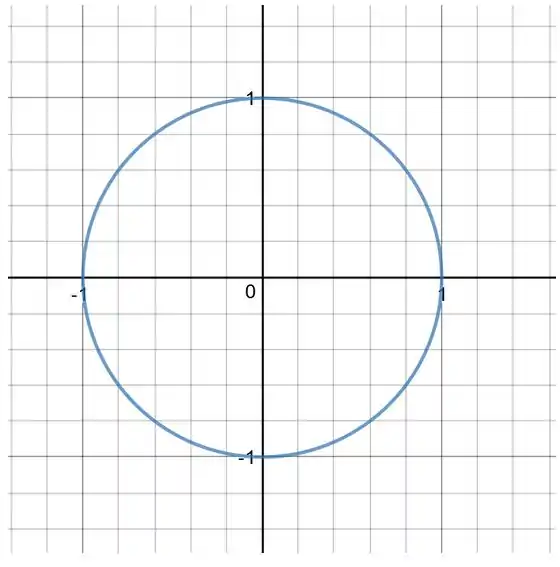
Executando a superposição dos projetos e trajetórias dos planos e para a solução de .
Passo 4
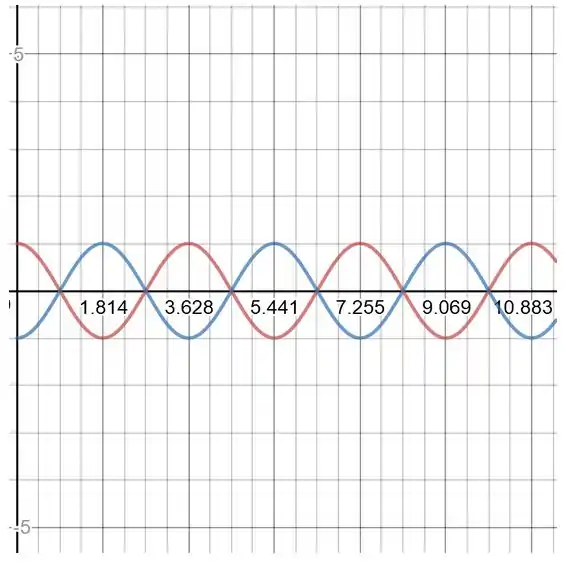
Executando o gráfico de versus e para solução .
Passo 5
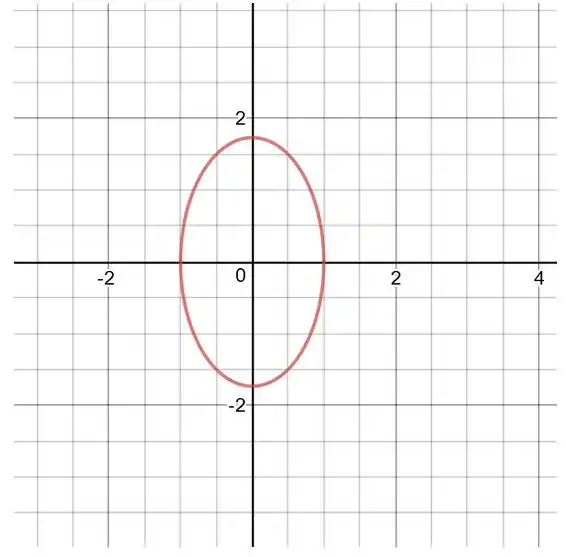
A superposição das projeções e trajetórias nos planos e para a solução .
Resposta
Ei, a resposta está no passo a passo :)