Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 4.4 - Ex. 11
Em cada um dos problemas de 9 a 12, encontre a solução do problema de valor inicial dado. Depois faça um gráfico da solução.
11.
Passo 1
Fala Galera!!
Para resolver essa questão, vamos começar pegando a equação ordinária dada no problema:
A equação homogênea correspondente é a seguinte:
Pensando nela, a nossa equação característica, terá o seguinte formato:
Dessa forma, temos então que as raízes da homogênea associada são:
Passo 2
Aqui, Temos então que a que as raízes da equação característica são , e . Assim, vemos que , e são as soluções da equação homogênea. Portanto, a solução para a homogênea associada é:
Passo 3
Precisamos agora encontrar uma solução particular para a para a equação diferencial fornecida, para isso, podemos usar o método de variação dos parâmetros. Assim, a solução específica é dada por:
Em que é a função da equação ordinária depois da igualdade na equação diferencial dado no começo, vem do determinante da matriz dos coeficientes
e é obtido desubstituindo a m-ésima coluna pela coluna
Passo 4
Vamos agora calcular . Assim temos:
Passo 5
Vamos agora calcular , para isso pegamos a matriz acima e trocamos a coluna 1 por . Assim temos:
Passo 6
Vamos agora calcular , para isso pegamos a matriz acima e trocamos a coluna 2 por . Assim temos:
Passo 7
Vamos agora calcular , para isso pegamos a matriz acima e trocamos a coluna 3 por . Assim temos:
Passo 8
Agora, vamos calcular a solução particular. Assim temos:
Passo 9
Vamos calcular os termos separadamente. Assim temos:
Substituindo temos:
Passo 10
Assim, podemos escrever a solução geral da seguinte forma:
Substituindo a solução da homogênea associada e a solução particular, temos:
Onde , e são constantes arbitrárias.
Passo 11
Podemos encontrar as constantes , e utilizando as condições iniciais.
As condições iniciais fornecidas são:
Usando a primeira condição temos:
Usando a segunda condição temos:
Usando a terceira condição temos:
Temos agora 3 equações e 3 variáveis:
Temos então que:
Substituindo na primeira equação:
Logo,
Substituindo na segunda equação temos:
Então
Passo 12
Portanto, a solução geral é obtida substituindo os valores encontras. Assim temos:
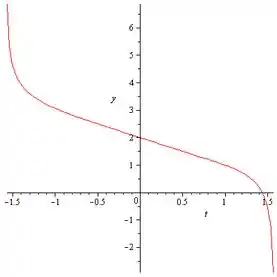
Passo 13
O gráfico da solução é apresentado abaixo:
