Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.1 - Ex. 7
Em cada um dos problemas de 7 a 12, encontre valores aproximados da solução do problema de valor
inicial dado em t = 0,5; 1,0; 1,5 e 2,0.
(a) Use o método de Euler com h = 0,025.
(b) Use o método de Euler com h = 0,0125.
(c) Use o método de Euler inverso com h = 0,025.
(d) Use o método de Euler inverso com h = 0,0125.
7)
Passo 1
Temos que o método de Euler fica:
Onde:
E a condição inicial:
Demonstrando o primeiro passo, temos:
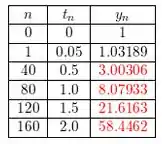
Repetindo os mesmo passos até chegar em , tendo a seguinte tabela:
Passo 2
b) Temos que o método de Euler fica:
Onde:
E a condição inicial:
Demonstrando o primeiro passo, temos:
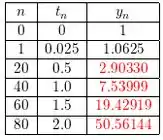
Repetindo os mesmo passos até chegar em , tendo a seguinte tabela:
c)Método de e Euler inverso, temos:
Onde:
E a condição inicial:
Demonstrando o primeiro passo, temos:
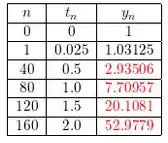
Repetindo os mesmo passos até chegar em , tendo a seguinte tabela:
Passo 3
d)
Método de e Euler inverso, temos:
Onde:
E a condição inicial:
Demonstrando o primeiro passo, temos:
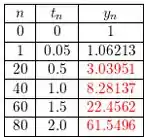
Repetindo os mesmo passos até chegar em , tendo a seguinte tabela:
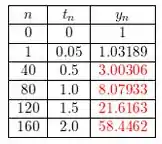
Resposta
a)
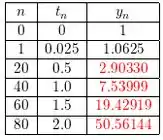
b)
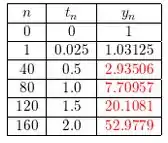
c)
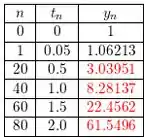
d)
