Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.3 - Ex. 12

Em cada um dos problemas de 7 a 12, encontre valores aproximados da solução do problema de valor inicial dado em t   =   0,5 ;   1,0 ;   1,5   e 2,0 . Compare os resultados com os obtidos usando outros métodos e com a solução exata (se disponível).

(a) Useo método de Runge-Kutta com h   =   0,1 .

(b) Useo método de Runge-Kutta com h   =   0,05 .

12. y ' = y 2 + 2 t y 3 + t 2 ,     y 0 = 0 , 5

Passo 1

Bora lá pro nosso primeiro probleminha sobre método de R u n g e - K u t t a .

Olha só! A nossa f ( t , y ) já sabemos que é dada por...

f t , y = y 2 + 2 t y 3 + t 2

E sabemos também das seguintes condições:

t n = t 0 + n h

y 0 = 1

Sabendo disso, é uma boa utilizarmos o método de 4 ª ordem pra resolver esse nosso problema. Assim, iremos obter valores mais aproximados em cada ponto pedido.

A nossa iteração no método de R u n g e - K u t t a de 2 ª   ordem é dada por...

y n + 1 = y n + 1 6 k 1 + 2 k 2 + 2 k 3 + k 4

Agora presta atenção! Como o objetivo é resolver esse problema computacionalmente, o que estamos procurando aqui é fórmulas pra colocarmos em nosso código. De preferência, que estejam em função de h e das condições fornecidas pelo enunciado.

Disso isso! Bora pro que interessa! Vamos obter k 1 ...

k 1 = h f ( t n , y n )

k 1 = h y n 2 + 2 t n y n 3 + t n 2

k 1 = h y n 2 + 2 n h y n 3 + n 2 h 2

Depois, bora descobrir k 2 , que é dado por...

k 2 = h f t n + 1 2 h , y n + k 1 2

k 2 = h y n + k 1 2 2 + 2 t n + 1 2 h y n + k 1 2 3 + t n + 1 2 h 2

k 2 = h y n + k 1 2 2 + 2 n h + 1 2 h y n + k 1 2 3 + n h + 1 2 h 2

Em seguida, bora partir pra obtenção de k 3   , que é igual à...

k 3 = h f t n + 1 2 h , y n + k 2 2

k 3 = h y n + k 2 2 2 + 2 t n + 1 2 h y n + k 2 2 3 + t n + 1 2 h 2

k 3 = h y n + k 2 2 2 + 2 n h + 1 2 h y n + k 2 2 3 + n h + 1 2 h 2

E finalmente, vamos obter k 4 ...

k 4 = h f t n + h , y n + k 3

k 4 = h y n + k 3 2 + 2 t n + h y n + k 3 3 + t n + h 2

k 4 = h y n + k 3 2 + 2 n h + h y n + k 3 3 + n h + h 2

Pronto! Agora vamos pegar esses dados pra usar em nossa resolução computacional.

Passo 2

Para isso, vamos usar a seguinte estrutura abaixo em forma de algoritmo...

P a s s o   1 : D e f i n i r   c a d a   f u n ç ã o   d e   i t e r a ç ã o   k n

P a s s o   2 : D e f i n i r   o   t a m a n h o   d o   p a s s o   e   d o   v a l o r   i n i c i a l   y ( 0 )

P a s s o   3 : F a z e r   n   r e c e b e r   0 ,   p a r a   q u e   e l e   v e n h a   a   s e r   i n c r e m e n t a d o   e m   n o s s o s   c ó d i g o

P a s s o   4 : P a r a   i   d e   1   a t é   u m   t a m a n h o   T A M   d e   2.0 h   f a ç a  

P a s s o   5 :  

k 1 = h y n 2 + 2 n h y n 3 + n 2 h 2

k 2 = h y n + k 1 2 2 + 2 n h + 1 2 h y n + k 1 2 3 + n h + 1 2 h 2

k 3 = h y n + k 2 2 2 + 2 n h + 1 2 h y n + k 2 2 3 + n h + 1 2 h 2

k 4 = h y n + k 3 2 + 2 n h + h y n + k 3 3 + n h + h 2

y n + 1 = y n + 1 6 k 1 + 2 k 2 + 2 k 3 + k 4

i = i + 1  

n = n + 1  

P a s s o   6 : E s c r e v a   ( y n + 1 )

P a s s o   7 : F i m

Captou a mensagem!?

Pois bora em frente!

Passo 3

a) Desse modo, utilizando uma linguagem de programação qualquer, C ou P y t h o n ... Você é quem sabe! É possível determinar o que a gente quer. No caso, bora usar a linguagem C ...

Olha só! O seguinte código abaixo foi feito...

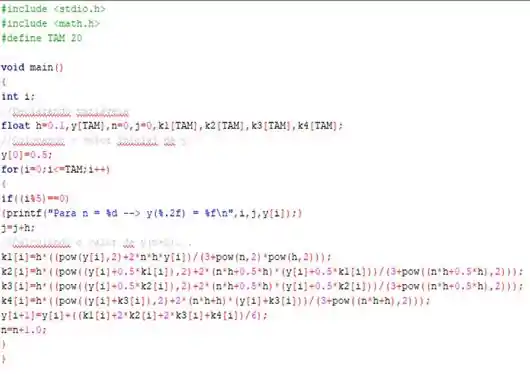
O legal é que esse código vai ser servir pra quase todas as questões desse seção! Só é preciso alterar um detalhe aqui e outro acolá!

Bom! Compilando ele, num total de iterações ( T A M ) igual à...

T A M = 2 h = 2 0.1 = 20

É importante ressaltar que botamos um condicional em nosso código para que ele p r i n t e apenas os valores que pede o enunciado. Podemos fazer isso, colocando um " i f " para que toda vez que a divisão de i por 5 for 0 , o programa mostrar.

Voltando ao assunto da compilação! Obtemos os seguintes valores da figura abaixo...

E de quebra, obtemos a seguinte tabela:

Passo 4

b) Já nessa letra, só basta alterar duas coisas no código confeccional. Primeiro, o valor de h   que vai ser igual a 0 . 05 .

E depois o tamanho T A M de iterações, que vai valer...

T A M = 2 0.05 = 40

Ah! Esqueci de falar! No condicional i f , dessa vez o nosso " i f " vai fazer com que toda vez que a divisão de i por 10 for 0 , o programa mostre o valor de y em j .

Desse modo, compilando o código com essas alterações... Obtemos os valores expostos na imagem abaixo:

Passo 5

E pra finalizar... Colocando a E D O em um software qualquer, tipo S y m b o l a b , obtemos que a solução exata dela é...

y = 3 + t 2 6 - t

Depois, vamos destacar alguns valores para ver se a nossa resolução computacional foi satisfatória.

Vamos testar para t = 0.5 ;

y = 3 + t 2 6 - t

y = 3 + ( 0.5 ) 2 6 - 0.5

y = 0.59090909

E depois, para t = 1.0 :

y = 3 + t 2 6 - t

y = 3 + ( 1.0 ) 2 6 - 1.0

y = 0.6666667

Para t = 1.5 :

y = 3 + t 2 6 - t

y = 3 + ( 1.5 ) 2 6 - 1.5

y = 1.16666667

Por último, para t = 2.0 :

y = 3 + t 2 6 - t

y = 3 + ( 2.0 ) 2 6 - 2.0

y = 1.75

Pronto! Vimos com isso que os valores reais se aproximam e muito dos que obtivemos através da nossa resolução computacional. Pra falar a verdade, são quase iguais, quase mesmo. Alguns são até iguais de fato.

Resposta

a)

b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 17 a 34, encontre todos os pontos singulares da equação dada e determine se cada um deles é regular ou irregular.17. x y ″+( 1–x ) y '+x y=0
Em cada um dos problemas de 17 a 34, encontre todos os pontos singulares da equação dada e determine se cada um deles é regular ou irregular.30. x 2 y ″+2 ( e x-1 ) y '+( e - xc o sx ) y=0
Em cada um dos problemas de 17 a 34, encontre todos os pontos singulares da equação dada e determine se cada um deles é regular ou irregular.32. x y ″+y '+( c o tx ) y=0
Em cada um dos problemas de 17 a 34, encontre todos os pontos singulares da equação dada e determine se cada um deles é regular ou irregular.33. ( s e nx ) y ″+x y '+4 y=0
Em cada um dos problemas de 17 a 34, encontre todos os pontos singulares da equação dada e determine se cada um deles é regular ou irregular.34. ( xs e nx ) y ″+3 y '+x y=0