Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.1 - Ex. 22
Em cada um dos problemas de 21 a 23
a) Desenhe um campo de direções para a equação diferencial dada. Como parece que as soluções se comportam quando t assume grandes valores? O comportamento depende da escolha do valor inicial a? Seja o valor de a no qual ocorre a transição de um tipo de comportamento para outro. Estime o valor de
b) Resolva o problema de valor inicial e encontre precisamente o valor critico de
c) Deescreva o comportamento da solução correspondente ao valor inicial
Passo 1
a)
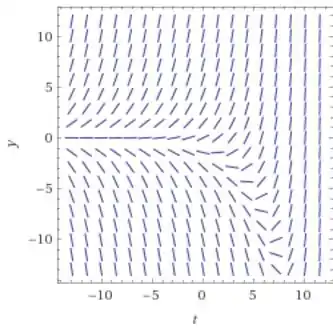
Passo 2
b)Vamos resolver pelo método...
Multiplicamos por
De modo que
Integrando nosso resultado acima( nesse passo, não incluímos a constante de integração ):
Repare que o lado esquerdo da nossa equação que foi multiplicada por é o resultado da regra do produto de derivação de 2 funcões
Subsituindo os valores encontrados e integrando
O problema de valor inicial será resolvido, usando a condição dada pelo problema
Passo 3
c)