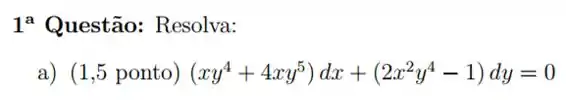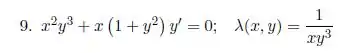Exercícios de Equação Não Exata - Fator Integrante - Lista de Exercícios Resolvida

Encontre um fator integrante e resolva a equação dada

Considere a equação diferencial

Determine todas as funções que tornam exata a equação diferencial

Encontre a solução geral da equação diferencial usando a achada no item .

Encontre um fator de integrante e resolva a equação:

Use o fator integrante para resolver:

Determine a solução:

Encontre um fator de integrante e resolva a equação:

Determine a solução geral da equação

Determine a solução geral da equação

Encontre a solução geral da equação diferencial dada.

c)

Encontre a solução geral da equação diferencial dada.

b)

Desenhar as curvas ou superfícies de nível dos seguintes campos escalares.

b.

Encontre um fator integrante e resolva a equação dada

Determine a solução geral da equação diferencial:

Encontre a solução geral da equação diferencial dada.

a)

Encontre a solução geral da equação diferencial dada.

d)

Achar a solução geral.

(a)

Achar a solução geral.

(b)

Achar a solução geral.

(c)

Achar a solução geral.

(e)

Resolva os PVI’s.

(c)

Achar a solução geral.

(f)

Resolva os PVI’s.

(a)

Resolva os PVI’s.

(b)

Resolva os PVI’s.

(e)

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(4)

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(1)

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(5)

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(6)

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(7)

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(9)

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(13)

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(12)

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(14)

Determine a solução geral da equação

Resolva as seguintes equações diferenciais, e problemas de valor inicial.

Nos exercícios a verifique se é possível encontrar um fator de integração do tipo ou que transforma a EDO dada em uma EDO exata. Em caso afirmativo, determine o fator de integração e resolva a EDO.

Nos exercícios a verifique se é possível encontrar um fator de integração do tipo ou que transforma a EDO dada em uma EDO exata. Em caso afirmativo, determine o fator de integração e resolva a EDO.

Nos exercícios a verifique que é um fator de integração que transforma a EDO dada em uma EDO exata e resolva a EDO.

Nos exercícios a verifique se é possível encontrar um fator de integração do tipo ou que transforma a EDO dada em uma EDO exata. Em caso afirmativo, determine o fator de integração e resolva a EDO.

Dada a equação diferencial , assinale a alternativa que contenha um fator integrante:

Encontre todas as soluções da EDO:

Considere o problema de valor inicial

Qual o limite de quando tende a ?

Dada a equação diferencial assinale a alternativa que contenha um fator integrante:

Dada a equação diferencial assinale a alternativa que contenha um fator integrante para essa equação:

Resolva a seguinte equação diferencial ou problema de valor inicial conforme caso abaixo:

Dada a equação diferencial assinale a alternativa que contenha um fator integrante para essa equação:

Encontre um fator integrante e resolva a equação diferencial

Resolva a equação diferencial homogênea

( )

( )

( )

( )

( )

Classifique e resolva a equação abaixo com o método apropriado.

Determine uma função de maneira que seja um fator integrante para a equação diferencial.

NÃO RESOLVA A EDO ACIMA!

Mostre que a EDO

não é exata, mas que se torna exata quando multiplicada pelo fator integrante

Determine, então, a solução geral da EDO.

Resolva as equações diferenciais:

Classifique e resolva a equação abaixo com o método apropriado.

Encontre um fator integrante e resolva a equação dada

Achar a solução geral.

(d)

1. Determine uma função de modo que

seja um fator integrante da equação diferencial

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(3)

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(8)

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(10)

Teste 4: Considere a equação

E as afirmações:

1. A equação é exata
2. A equação admite um fator integrante .
3. A equação possui um fator integrante e a função é um potencial correspondente.

São verdadeiras:

1. Apenas .
2. Apenas e .
3. Todas.
4. Nenhuma.
5. Apenas .

Ao encontrar um fator integrante da forma de modo a tornar exata a equação diferencial, descreva suas soluções:

Considere a solução particular da equação tal que . Então, é:

Escolha uma:

Nos exercícios a verifique se é possível encontrar um fator de integração do tipo ou que transforma a EDO dada em uma EDO exata. Em caso afirmativo, determine o fator de integração e resolva a EDO.

Nos exercícios a verifique se é possível encontrar um fator de integração do tipo ou que transforma a EDO dada em uma EDO exata. Em caso afirmativo, determine o fator de integração e resolva a EDO.

Se é um fator integrante para a equação diferencial , então ?

Nos exercícios a verifique se é possível encontrar um fator de integração do tipo ou que transforma a EDO dada em uma EDO exata. Em caso afirmativo, determine o fator de integração e resolva a EDO.

Considere o problema de valor inicial

Qual o limite de quando tende a ?

Dada a equação diferencial assinale a alternativa que contenha uma solução dessa equação:

Resolva os PVI’s.

(c)

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(2)

Para cada uma das EDOs a seguir, verifique que ela é não-exata; determine então um fator integrante g, função de somente uma das variáveis; e a seguir obtenha a solução geral da EDO.

(11)

Verifique se a equação dada é exata. Em caso negativo, encontre o fator integrante que transforma a equação dada em uma equação exata. Resolva o problema de valor inicial.

) Seja uma constante. Encontre uma solução para o PVI

) É possível escolher a constante de modo a garantir que conforme ?

Considere o problema de valores iniciais:

1. Encontre um par de funções e tal que as soluções o PVI convergem para conforme tende ao infinito. I.e.

2. Encontre um par de funções e tal que as soluções o PVI convergem para conforme tende ao infinito. I.e.,

3. Em cada um dos itens acima, o que acontece se ?

Considere o problema de valor inicial

Qual o limite de quando tende a ?

Considere a seguinte EDO:

Encontre, se possível, um fator integrante que transforme a equação dada em uma equação exata ( só depende da variável ).

Considere a seguinte EDO:

Mostre que esta equação não é exata.

No seu livro de Cálculo de 1696, ilustrou sua regra com o limite da função

Quando . Calcule o valor deste limite.

Resolva as equações diferenciais:

Resolva as equações diferenciais:

Resolva as equações diferenciais:

Resolva as equações diferenciais:

Resolva as equações diferenciais:

Resolva as equações diferenciais:

Resolva as equações diferenciais:

Resolva as equações diferenciais:

Seja uma solução particular da equação diferencial . Calcular

Determine uma equação diferencial ordinária de primeira ordem tal que

Resolva as equações diferenciais:

Resolva as equações diferenciais:

Seja uma função tal que . Calcule

Achar um fator integrante da equação

Determine a solução geral da equação

Sabendo que ela tem um fator integrante que só depende de

Considere a equação diferencial . Se é uma solução desta equação diferencial para a qual existe então calcule o limite

Nos exercícios a verifique se é possível encontrar um fator de integração do tipo ou que transforma a EDO dada em uma EDO exata. Em caso afirmativo, determine o fator de integração e resolva a EDO.

Para cada equação, determine se ela é exata. Se for, encontre a solução:

a)

Dada a equação diferencial , assinale a alternativa que contenha um fator integrante:

Questão 3: (Justifique todas as suas respostas)

1. Decida se a equação abaixo é exata:

Justifique todos os passos do seu argumento!

2. Caso a equação não seja exata, utilize o fator integrante para encontrar uma solução.

Considere o problema de valor inicial

Qual o limite de quando tende a ?

Considere o problema de valor inicial

Qual o limite de quando tende a ?

Resolva a seguinte equação diferencial ou problema de valor inicial conforme seja o caso:

(b)

Determine a solução do problema de valor inicial:

Um fator integrante para a equação diferencial é ?

Calcule a derivada de

usando a definição de derivada.

Sejam um número real fixado e uma função derivável. Sabendo que e , determine o valor de .