Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 21
Uma caixa aberta deve ser feita com uma folha de metal de por , cortando-se quadrados iguais dos quatro cantos e dobrando-se os lados. Encontre o volume máximo que uma caixa dessas pode ter.
Passo 1
Vamos refletir, olhando o desenho abaixo:
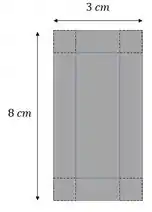
Temos essa folha aí, vamos tirar esses quadradinhos pontilhados da folha e dobra-lá para fazer uma caixa. Queremos descobrir o volume máximo da caixa.
Para descobrir isso, a gente precisa encontrar uma função que descreve o volume e descobrir o maior valor dela.
Vamos tentar fazer isso!
Passo 2
Vamos chamar os lados desses quadradinhos de :
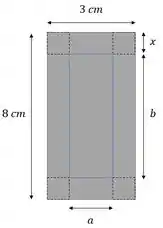
Vamos imaginar que já tiramos os quadradinhos e dobramos a caixa. Olhando a figura, volume dela é dado pela expressão:
Passo 3
A gente também pode escrever uma expressão para e , olhando nossa figura:
E:
Reescrevendo o volume:
E como é uma dimensão, ele dever ser maior que zero.
Passo 4
Com a expressão do volume, podemos tentar descobrir o valor máximo dela. Vamos verificar os valores de onde .
Vamos derivar essa função da área e igualar a zero:
Igualando a zero:
Resolvendo essa equação do segundo grau:
Como são todos positivos, esses serão os nossos candidatos para .
Passo 5
Agora para descobrir qual é o maior volume, a gente precisa jogar esses valores de na nossa expressão para o volume:
Logo, o nosso volume máximo ocorre em e o volume máximo é: