Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.1 - Ex. 60
Encontre uma fórmula para a função descrita e obtenha seu domínio.Uma caixa retangular fechada com volume de tem comprimento igual duas vezes a largura. Expresse a altura da caixa como função da largura.
Passo 1
Falaee, belezinha?? Bom... a questão quer que encontremos uma fórmula para a altura de uma caixa em função de sua largura.
Para isso a questão nos diz que a caixa retangular fechada com volume de tem comprimento igual duas vezes a largura.
Nesse sentido, vamos supor que nossa caixa retangular mostrada abaixo tem altura , largura e comprimento :
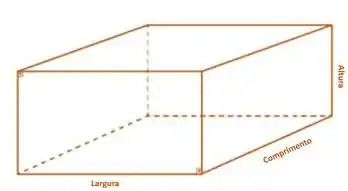
Para encontrarmos a fórmula da altura que queremos, temos que fazer algumas relações envolvendo o volume da caixa.
E aí? Bora lá?? 😉
Passo 2
Pelo que sabemos, temos que seu volume é dado por:
A questão nos diz que seu volume é de , portanto:
Vale lembrar que o seu comprimento é duas vezes a sua largura, logo:
Agora vamos juntar os dados para encontrarmos a fórmula da altura!! 😉
Passo 3
Substituindo na fórmula do volume, temos:
Isolando :
Passo 4
E o domínio são todos os valores para os quais existe.
Nesse caso, por se tratar de um quociente, o denominador não pode ser zero!
Assim, o domínio são todos os números reais tal que . Ou matematicamente falando, temos:
Até porque, se a largura for 0, não vamos ter uma caixa né!
Entendeu direitinho?? Responde aee 😉