Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 66
Uma empresa de eletricidade cobra de seus clientes uma taxa-base de mensais, mais 6 centavos por quilowatt-hora () para os primeiros e centavos para todo uso acima de . Expresse o custo mensal como uma função da quantidade utilizada de eletricidade. Então, faça um gráfico da função para .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente construir uma expressão para o custo mensal em função da quantidade de eletricidade utilizada e fazer um gráfico dessa função .
Pra isso, ele nos disse que a empresa cobra de seus clientes uma taxa-base de mensais, mais 6 centavos por quilowatt-hora () para os primeiros e centavos para todo uso acima de .
Então, se você contratar o serviço, mesmo que você consuma apenas , você terá que pagar uma taxa de mais vezes a quantidade de consumido, mas isso só se você consumir menos que Se você consumir mais do que isso, será cobrada uma taxa de vezes a quantidade de consumido. Então, vamos expressar isso matematicamente.
Passo 2
Na primeira situação, onde consumimos menos do que , temos a taxa de centavos por cada consumido, mais um valor fixo de . Representando isso em termos matemáticos, temos:
Lembrando que representa a quantidade de eletricidade naquele mês.
Então, o custo da energia para os primeiros consumido será (quando :
Até aí tudo bem, mas e se você consumir mais que ?
Conforme o enunciado, teremos mais 7 centavos para todo uso acima de . O que isso quer dizer? Quer dizer que se você consumir você pagará os , ou seja, aqueles dolares pelos primeiros mais 7 centavos pelo (que foi o uso acima dos . Sacou?
Então, representando isso, temos:
Passo 3
Agora que entendemos como que funciona o pagamento para ambos os casos, vamos organizar e definir nossa função direitinho, beleza?
Como fazemos isso? É só juntar tudo que descobrimos até agora.
Assim, temos a função definida por partes:
Passo 4
Você já ia indo embora?
Ainda falta esboçar o gráfico. Vamos lá!
Temos uma reta , para menor ou igual a , e outra reta , para maior do que . Então, nosso gráfico fica assim:
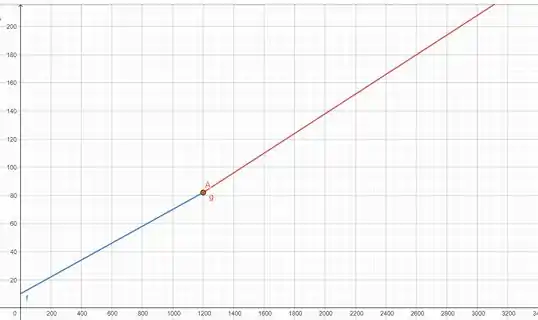
Valeu, galera! Até a próxima! 😉