Uma caixa sem a tampa deve ser construída de um pedaço retangular de papelão com dimensões por polegadas. Devem-se cortar os quadrados de lados de cada canto e depois dobrar, conforme mostra a figura. Expresse o volume da caixa com uma função de .
James Stewart - Vol 1 - 6ª Ed - Ed.5 - Capítulo 1 - Seção 1 - Exercício 53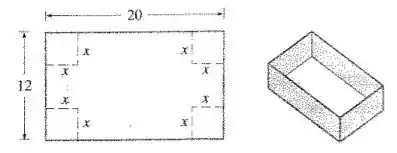
Passo 1
Opa, bora lá! O enunciado nos dá o desenho pra construção de uma caixa:
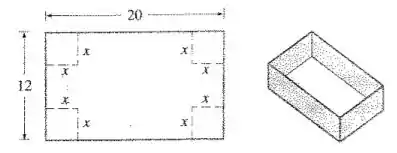
Desejamos expressar o volume dessa caixa (que tem o formato de um paralelepípedo) em função da medida . Primeiramente devemos nos lembrar que o volume de um paralelepípedo é dado multiplicando-se as medidas: altura, largura e comprimento; sendo assim, o que devemos fazer é encontrar essas medidas para a nossa caixa. Vamos começar, então, pelo comprimento:
- Inicialmente tínhamos um comprimento de , mas veja que foram removidos quadrados de lado dele o que faz com que ficamos com como comprimento;
- Agora vamos para a largura que vai basicamente a mesma ideia do comprimento, mas adivinha só? com a largura; como tínhamos uma largura de iniciais e removemos quadrados de lado encontramos como largura agora ;
- Por fim, o mais simples de imaginar: a altura; temos que o lado dos quadrados que foram removidos serão, exatamente, nossa altura da caixinha;
Portanto, temos agora todas as medidas necessárias para calcularmos o volume de interesse.
Passo 2
Dadas as dimensões acima, ficou muito simples resolver esse problema e você pode se pensar: “duvido muito” e eu te mostro, veja só:
Agora a gente só precisa dar uma arrumadinha:
Prontinhoo!