Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.1 - Ex. 44
Encontre uma expressão para a função cujo gráfico é a curva dada. A parte de cima do círculo
Passo 1
Opa, bora lá! Queremos encontrar a expressão para a função que representa a parte de cima do círculo:
Para isso vamos lembrar que a equação do círculo pode ser representada por:
Onde e são as coordenadas do centro do círculo e é o tamanho do raio.
Também vamos fazer alguma manipulações na equação, como isolar o ou o . Vai depender do que queremos.
Então, olhando pra equação do enunciado e comparando termo a termo, temos as coordenadas do centro e o raio:
E podemos até representar esse círculo num gráfico:
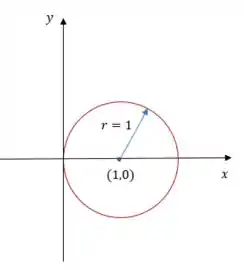
Passo 2
Repara que a parte de cima do círculo é quando é positivo (está acima da reta do ), então vamos isolar o :
Atençãooo... não esqueça que quando passamos o quadrado pro outro lado virando raiz, ele vira “mais ou menos” a raiz....
Maaaaas, queremos exatamente os valores positivos de , certo? (lembrando a raiz quadrada é seeempre igual a zero ou positiva) Então:
Calma que ainda não acabou... Falta um detalhezinho.
Se deixarmos só essa resposta estaremos dizendo que todos os valores de servem, maaas os valores de são limitados pelo próprio círculo. Olha de novo pra figura:
Então enxergamos que o varia de até . Escrevendo isso em forma de intervalo:
Então nossa resposta final fica:
com .
Resposta
com .