Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 63
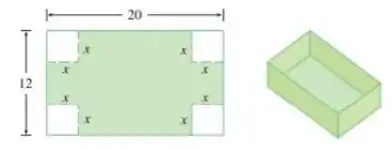
Uma caixa sem tampa deve ser construída de um pedaço retangular de papelão com dimensões cm por cm. Para isso, deve-se cortar quadrados de lados x de cada canto e depois dobrar, conforme mostra a figura. Expresse o volume V da caixa como uma função de x.
Passo 1
Eaee, belezinha??
Bom... queremos encontrar uma expressão do volume da caixa em função de , que são quadrados de cada canto da caixa, como mostra a figura abaixo:
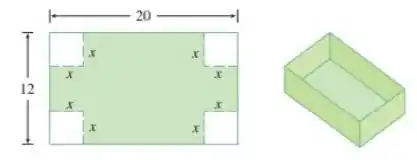
Para isso, temos que relacionar as medidas do papelão com as medidas da caixa.
Se você reparar bem, quando dobramos o papelão, esse tamanho vai se tornar a altura da caixa. Hmmm, agora a gente começa a ver alguma coisa ne?
E aí?? Bora lá?? 😉
Passo 2
Bom... Os quadrados que serão recortados possuem lado . Então, cada lado da base da caixa vai ficar menor que os lados do papelão em .
Dessa forma, a base da caixa terá dimensões de , e sua altura será .
Nesse sentido, o volume da caixa será dado pela multiplicação das arestas (comprimento, largura e altura):
Assim, temos a nossa função !!!
Entendeu direitinho?? Responde Aí 😉
