Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 1
Explique com suas palavras o significado da equação:
É possível que a equação anterior seja verdadeira, mas que ? Explique
Passo 1
A questão pediu pra você explicar com as suas palavras mas vamos explicar aqui com as nossas, ok? Hahahha
Ai se você pescar a ideia, vai estar pronto pra explicar com as suas. A equação:
Pode ser lida como: “A função tende ao valor quando se aproxima de ”. Isso quer dizer que quanto mais pertinho de chega, mais pertinho de nosso fica.
Um exemplo tranquilin desse fenômeno pode ser mostrado na tabela abaixo:
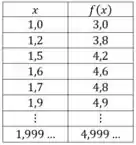
Importante dizer que não necessariamente essa equação implica em , apesar de ser uma possibilidade, dependendo de quem for .
Passo 2
Nesse próximo passo a gente vai responder a segunda pergunta da questão: É possível que a equação anterior seja verdadeira, mas que ? Bem, vamos pensar no seguinte, como a definição de limite tem a ver com aproximação de a um valor e aproximação de a outro valor, como dito no final do passo anterior:
Portanto, imaginando um caso loko como esse:
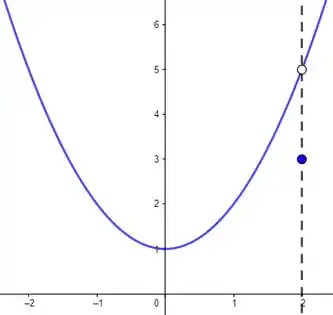
Vai ser uma verdade tanto:
Quanto:
Afinal, o ponto que normalmente participaria da curva foi removido, por não estar definido. No lugar dele, que está definido.Portanto é sim possível!
Mas atenção, o limite é possível. Mas nesse caso a função não será contínua!
Resposta
Desenvolvimento acima